この記事では、Arweaveの最新のホワイトペーパーの第3節を紹介します。この部分では、いくつかの基本的な概念について説明し、その後のメカニズムの紹介のための基盤を築きます。本来、この部分にはSPoResのメカニズムの証明も含まれていましたが、すべてが数式と数学的な推導の過程であるため、著者は別に解説する方がより合理的だと考えました。

Arweaveのマイニングメカニズムは、多くの異なるアルゴリズムとデータ構造を組み合わせて、非対話型で簡潔なデータ複製ストレージ証明を形成しています。本記事では、まずメカニズムの概念を抽象的に理解し、その後、Arweaveのマイニングプロセスにおけるそれらの使用について説明します。

ホワイトペーパーのリンク：https://www.arweave.org/files/arweave-lightpaper.pdf

ブロックインデックス

Arweaveにおける最高のデータ構造はブロックインデックス（Block Index）と呼ばれています。これは三元組（3-tuples）からなるマークル化リストであり、各タプルは3つの次元の情報を含んでいます。すなわち、ブロックハッシュ（A Block Hash）、織りネットワークのサイズ（A Weave Size）、およびトランザクションルート（A Transaction Root）です。このリストはハッシュマークルツリーの形式で表され、最上部のマークルルートはネットワーク内の現在の最新の状態を示します。このルートは、2つの要素のハッシュから構成されます------最新のタプル（最新のブロックを表す）と前のブロックインデックスのマークルルートです。ブロックを作成する際、マイナーは前のブロックインデックスのマークルルートを新しいブロックに埋め込みます。

各ブロック内にブロックインデックスのマークルルートを構築し埋め込むことで、最新のブロックに対してSPV証明を実行したArweaveネットワークノードは、以前のブロックを完全に検証することができます。これは従来のブロックチェーンと対照的で、従来のブロックチェーンでは古いブロック内のトランザクションを検証するために、全体のチェーンを遡って完全な検証を行う必要があります。しかし、Arweaveでは、ネットワークの最上部に対してSPV検証を行った後、ブロックインデックス検証メカニズムにより、ユーザーはネットワークの最上部に対してSPV検証を行った後に織りネットワーク内の古いブロックを検証でき、中間のブロックヘッダーをダウンロードまたは検証する必要がなくなります。

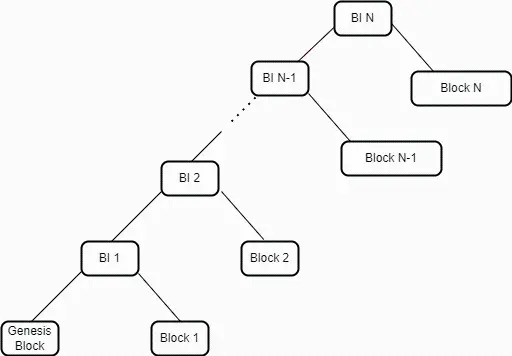
図1：ブロックインデックスはArweaveネットワーク内のブロックのマークルツリーを表しています。

マークル化データ

データはどのようにネットワークに保存されるのでしょうか？

情報がArweaveに保存される必要があるとき、データは規格に従って256KBのデータブロック（Chunk）に分割されます。これらのデータブロックが準備できると、マークルツリーが構築され、そのルート（データルート Data Rootと呼ばれる）がトランザクションに提出されます。このトランザクションは署名され、アップローダーによってネットワークに送信されます。このように構築された各トランザクションは、その所属するブロックのトランザクションルート（Transaction Root）に記録されます。したがって、1つのブロックのトランザクションルートは実際にはトランザクションデータルートのマークルルートです。

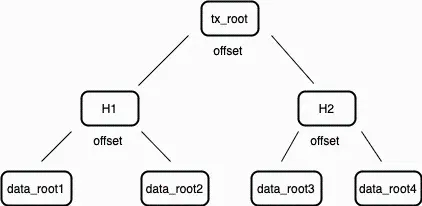
図2：トランザクションルートはブロック内の各トランザクションに存在するデータルートのマークルルートです。

マイナーはこのようなトランザクションを組み合わせて1つのブロックを作成し、トランザクション内のデータルートを使用してトランザクションルートを計算し、このトランザクションルートを新しいブロックに含めます。このトランザクションルートは最終的に最上部のブロックインデックスに現れます。このプロセスは、すべてのデータが順番にデータブロックに分割された、拡張し続けるマークルツリーを作成します。

簡潔なアクセス証明 SPoA

Arweaveネットワークでは、マークルツリー内のノードは、ノードの「左側」または「右側」のオフセット位置をマークすることでデータブロックをマークします。このようなノードのマーク方法は、特定の位置におけるデータブロックの存在を検証するための非常に簡潔なマークル証明を生成することができます。この種のマークルツリーは「不均衡ツリー」と呼ばれ、ノードの一方の葉ノードの数がもう一方と等しくない可能性があります。この構造は、マイナーのハードディスクに実際に対応するデータが存在することを検証するための簡潔な非対話型証明ゲームを構築するために使用できます。

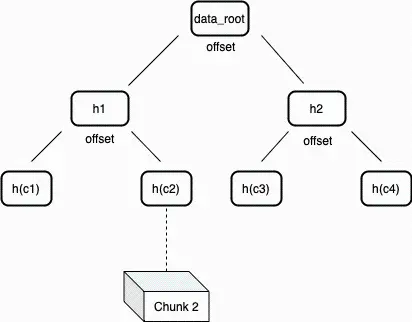
図3：データルート（data root）は単一のトランザクション内のすべてのデータブロックがハッシュ処理されたマークルルートです。

私たちはボブとアリスのゲームを通じて、簡潔なアクセス証明（Succint Proof of Access SPoA）とは何かを理解します。ボブはアリスがマークル化データセットの特定の位置にデータを保存しているかどうかを検証したいと考えています。ゲームを開始するために、ボブとアリスは同じデータセットのマークルルートを持っている必要があります。ゲームは3つの段階に分かれています：挑戦、証明構築、検証。

• 挑戦：ボブはアリスにデータブロックのオフセット（データブロックの位置座標として理解するとより明確です）を送信して挑戦を開始します------アリスはこの位置インデックスのデータにアクセスできることを証明する必要があります。

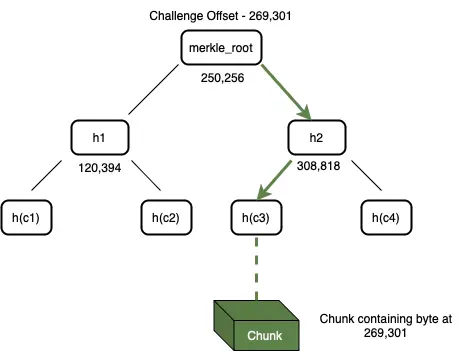
図4：アリスはオフセットラベルの付いたマークルツリーを遍歴して挑戦されたデータブロック（Chunk）を検索できます。

• 証明構築：この挑戦を受け取った後、アリスは証明を構築し始めます。彼女は自分のマークルツリーを検索し、オフセットに対応するデータブロックを見つけます（図4参照）。証明構築の第一段階では、アリスはストレージから全体のデータブロックを取得します。その後、彼女はそのデータブロックとマークルツリーを使用してマークル証明パスを構築します。彼女は全体のデータブロックをハッシュ処理して32バイトの文字列を取得し、ツリー内でこの葉ノードの親ノードを見つけます。親ノードは、そのオフセットと2つの子ノードのハッシュ値を含むノードであり、各ハッシュ値は32バイトの長さです。この親ノードが証明に追加されます。その後、各上位の親ノードを再帰的に証明に追加し、マークルルートに達するまで続けます。この一連のノードがマークルパス証明を形成し、アリスはこの証明をデータブロックと共にボブに送信します。

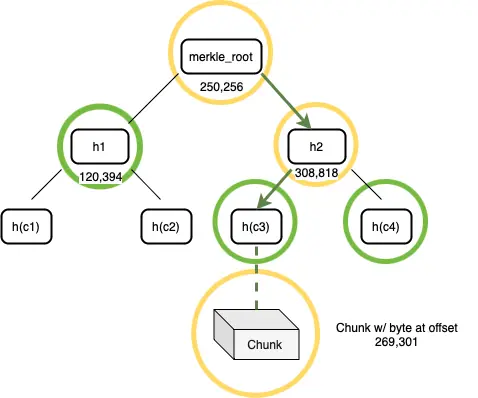
図5：挑戦オフセットの証明には、オフセットに保存されたデータブロックとそのマークルパスが含まれます。

• 検証：ボブはアリスからのマークル証明とデータブロックを受け取ります。彼はツリーの頂点から葉のハッシュ値を一つずつ確認することでマークル証明の正確性を検証します。次に、彼はアリスが提供した証明内のデータブロックをハッシュ計算し、このデータブロックが正しい位置にあるデータブロックであるかどうかを確認します。これらのハッシュ値がすべて一致すれば、証明は有効です。しかし、検証中にハッシュ値が一致しないことが発見された場合、ボブはすぐにチェックを停止し、アリスの証明が無効であると判断します。この検証の結果は、証明が通過したかどうかを示す単純な「はい」または「いいえ」のプロセスです。

この簡潔なアクセス証明（SPoA）の構築、伝送、検証の複雑さはO(logn)であり、ここでnはデータセットのサイズ（バイト単位）を表します。実際には、サイズが2の256乗バイトのデータセットにおいて、単一のバイトの位置と正確性の証明は、わずかに256 * 96B（最大パスサイズ）+ 256 KB（最大データブロックサイズ）≈ 280 KBで伝送できます。

コピーの唯一性

Arweaveネットワークは、マイニング能力をマイナー（または一組の協力するマイナー）がアクセスできる織りネットワークのコピーの数に比例するように設計しています。コピーの唯一性の仕組みがない場合、データのバックアップは内容的に完全に同じです。単一のデータの複数の唯一のコピーを奨励し、測定するために、Arweaveはこの問題を解決するためにパッキング（Packing）システムを使用しています。

パッキング Packing

パッキングメカニズムは、マイナーが同じデータブロックを使用して複数のSPoA証明を偽造できないようにします。ArweaveはRandomXパッキングスキームを引用し、元のデータブロックを「パッキング」されたデータブロックに変換します。このプロセスはマイナーに一定の計算コストをもたらします。

パッキングの流れは次の通りです：

• データブロックのオフセット、トランザクションルート、およびマイニングアドレスがSHA-256ハッシュに使用され、パッキングキーPacking Keyが生成されます。
• パッキングキーはアルゴリズムのエントロピーとして使用され、数ラウンドのRandomX実行後に2MBのレジスタが生成されます。このパッキングメカニズムの構成要素は、ルールを守らないマイナーにとって重大なコストをもたらします。
• このエントロピーの最初の256KBは、フェイステル暗号（Feistel cypher）を使用してブロックを対称的に暗号化するために使用されます。これにより、パッキングデータブロックが生成されます。

連続して読み取る時間周期内で、パッキングデータブロックの総コストが保存されたデータブロックのコストを超えた場合、マイナーはユニークなデータブロックを保存するように奨励され、必要に応じてデータブロックをパッキングするのではなくなります。したがって、この正しい行動を奨励するためには、次の条件を満たす必要があります：

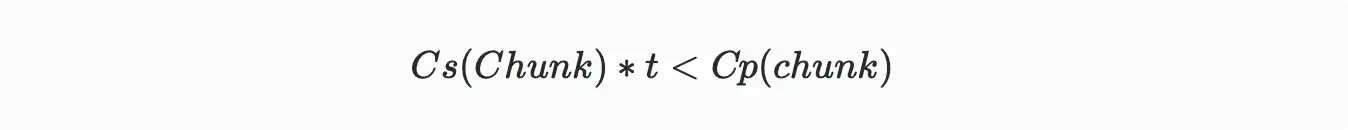
ここで：

Cs= データブロックを保存するための単位時間コスト

Cp= データブロックをパッキングするコスト

t= データブロックの読み取り間の平均時間

パッキングの総コストには、計算に必要な電力コスト、専用ハードウェアコスト、その平均使用寿命が含まれます。保存コストも、ハードディスクのコスト、ハードディスクの平均故障時間、ハードディスクを運用するための電力コスト、およびストレージハードウェアの運用に関連する他のコストから計算できます。「必要に応じて」投機的なマイナーと、パッキングデータブロックを保存する誠実なマイナーのコスト比率を計算することで、パッキングデータブロックを奨励する安全マージンを推定できます。実際、Arweaveは安全比率を使用しており------すなわち、必要に応じて投機的なマイニングコストとデータを保存する誠実なマイニングコストの比率------執筆時点で約19:1です。

RandomX

ハードウェア加速戦略に対抗するために、ArweaveはハッシュアルゴリズムRandomXを使用してパッキングキーを処理します。RandomXは汎用CPUに最適化されており、ハッシュ処理中にランダムなコード実行とさまざまなメモリ集約型技術を実施することで、専用ハードウェア（GPUやASICなど）の計算効率を大幅に制限します。

RandomXはランダムに生成されたプログラムを使用し、汎用CPUのハードウェア特性と高度に一致させます。これは、RandomXのハッシュ速度を向上させる唯一の方法が、より高速な汎用CPUを開発することを意味します。これは理論的にはより高速なCPUの開発を促進する動機となるかもしれませんが、実際には既存のCPU速度向上の動機に対して、この動機がもたらす影響はほとんど無視できるものです。

検証可能な遅延関数 VDF

検証可能な遅延関数（Verifiable Delay Function VDF）は、検証可能な暗号デジタル時計のようなもので、イベント間の時間の経過を計算して検証することを可能にします。VDFは、指定された数のハッシュ計算を順番に非並列で実行する必要があり、ユニークで効率的に検証可能な出力を生成します。Arweaveプロトコルは、VDFを生成するために「ハッシュチェーン（Hash Chain）」と呼ばれる技術を使用し、その再帰的定義は次のようになります：

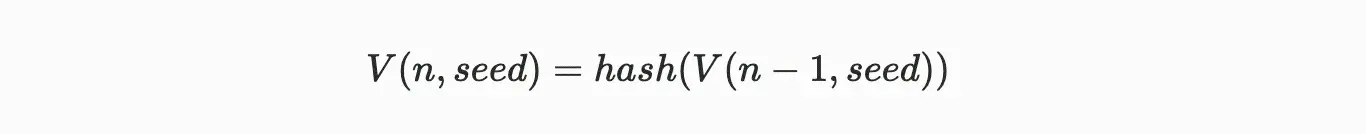
公式注釈：n番目のVDFハッシュは、その前のVDFハッシュの再ハッシュ処理です。

n = 1の場合：

公式注釈：n=1、すなわち最初のVDFハッシュは種子のハッシュ計算です。

Arweave VDFで使用されるハッシュ関数はSHA2-256です。この構造により、市場で最も高速なCPUプロセッサが毎秒k個のSHA2-256ハッシュ値を連続して計算できる場合、種子（seed）に対するV(k,seed)計算には少なくとも1秒の時間が必要です。これは連続ハッシュのプロセスであり、上記の公式に示されているように、n=1の場合はSeedをハッシュ計算し、n=2の場合はV（2，seed）がV（1，seed）のハッシュ計算となります。このように続きます。正しく生成されたV(k,seed)はチェックポイント（Checkpoint）と呼ばれ、証明者が種子を受け取り、このチェックポイントを生成する間に少なくとも1秒の時間が経過したことを意味します。

もしVDF構造がO(n)時間を要してnステップの計算を完了する必要がある場合、検証者はp個の並列スレッドを使用してO(n/p)時間内にVDF出力の検証を完了できます。ここで注意が必要なのは、VDFの生成には並列スレッド計算を使用してはいけませんが、検証は可能であり、これにより検証プロセスがより迅速かつ効率的になります。私たちがチェーン式ハッシュVDFを使用する理由は、その単純な構造と、ハッシュ関数の堅牢性に完全に依存している特性です。