Zk-SNARKs: Under the Hood

Author: Vitalik Buterin

Original Title: 《Zk-SNARKs: Under the Hood》

Published on: February 1, 2017

This is the third part of a series of articles explaining how the technology behind zk-SNARKs works; previous articles on quadratic arithmetic programs and elliptic curve pairings are essential reading, and this article will assume knowledge of these two concepts. It also assumes a basic understanding of what zk-SNARKs are and what they do. See also Christian Reitwiessner's article here for another technical introduction.

In previous articles, we introduced quadratic arithmetic programs, a method of representing any computational problem using polynomial equations that is more amenable to various forms of mathematical techniques. We also introduced elliptic curve pairings, which allow for a very limited form of one-way homomorphic encryption that lets you perform equality checks. Now, we will pick up where we left off last time, using elliptic curve pairings along with some other mathematical techniques to allow a prover to prove they know a solution to a specific QAP without revealing anything about the actual solution.

This article will focus on the Pinocchio protocol by Parno, Gentry, Howell, and Raykova that started in 2013 (commonly referred to as PGHR13); the basic mechanism has some variations, so the zk-SNARK schemes implemented in practice may differ slightly, but the fundamental principles generally remain the same.

First, let’s delve into the key cryptographic assumptions behind the security of the mechanism we will be using: the Knowledge of Exponent (KoE) assumption.

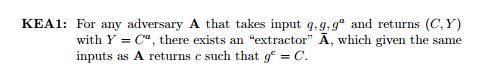
Essentially, if you have a pair of points P and Q such that P * k = Q, and you have a point C, then unless C is somehow "derived" from P, it is impossible to deduce C * k that you know. This may seem intuitive, but this assumption cannot actually be derived from any other assumptions we typically use when proving the security of elliptic curve-based protocols (such as the hardness of the discrete logarithm), so zk-SNARKs actually rely on a more unstable foundation than elliptic curve cryptography—though it is still robust enough that most cryptographers accept it.

Now, let’s see how to use it. Suppose there is a pair of points (P, Q) that fell from the sky, where P * k = Q, but no one knows what the value of k is. Now, suppose I present a pair of points (R, S) such that R * k = S. The KoE assumption means that the only way I could derive this pair of points is by taking P and Q and multiplying both by some factor r that I personally know. Also, note that due to the magic of elliptic curve pairings, checking R = k * S does not actually require knowing k—instead, you can simply check e(R, Q) = e(P, S).

Let’s do something more interesting. Suppose we have ten pairs of points that fell from the sky: (P1, Q1), (P2, Q2)… (P10, Q10). In all cases, Pi * k = Qi. Suppose I then provide you with a pair of points (R, S) such that R * k = S. What do you know now? You know that R is some linear combination P1 * i1 + P2 * i2 + … + P10 * i10, where I know the coefficients i1, i2 … i10. That is to say, the only way to obtain such a pair of points (R, S) is to take some multiples of P1, P2…P10 and add them together, and then do the same with Q1, Q2…Q_10.

Note that given any specific set of points P1…P10 you might want to check linear combinations of, you cannot actually create the accompanying Q1…Q10 points without knowing what k is. If you do know what k is, then you can create a pair (R, S) such that R * k = S for any R you want, without creating a linear combination. Therefore, to make this work, it is absolutely necessary to ensure that the person creating these points is trustworthy and that k is actually deleted after creating the ten points. This is the origin of the concept of "trusted setup."

Remember that the solution to a QAP is a set of polynomials (A, B, C) such that A(x) * B(x) - C(x) = H(x) * Z(x), where:

• A is a linear combination of a set of polynomials {A1…Am}
• B is a linear combination of {B1…Bm} with the same coefficients
• C is a linear combination of {C1…Cm} with the same coefficients

The sets {A1…Am}, {B1…Bm}, and {C1…Cm} along with the polynomial Z are part of the problem statement.

However, in most practical cases, A, B, and C are very large; for something like a hash function with thousands of circuit gates, the polynomials (and the factors of the linear combinations) can have thousands of terms. Therefore, instead of having the prover provide the linear combinations directly, we use the techniques we introduced above to have the prover prove that what they provided is a linear combination without revealing anything else.

You may have noticed that the above technique applies to elliptic curve points rather than polynomials. Therefore, what actually happens is that we add the following values to the trusted setup:

G * A1(t), G * A1(t) * ka G * A2(t), G * A2(t) * ka
…
G * B1(t), G * B1(t) * kb G * B2(t), G * B2(t) * kb
…
G * C1(t), G * C1(t) * kc G * C2(t), G * C2(t) * kc
…
You can think of t as the "secret point" for computing the polynomials. G is a "generator" (some random elliptic curve point designated as part of the protocol), and t, ka, kb, and kc are "toxic waste" numbers that must absolutely be deleted at all costs, or the person who has them will be able to create fake proofs. Now, if someone gives you a pair of points P, Q such that P * ka = Q (reminder: we do not need ka to check this, as we can do the pairing check), then you know that what they gave you is a linear combination of the Ai polynomials evaluated at t.

Thus far, the prover must provide:

πa = G * A(t), π'a = G * A(t) * ka πb = G * B(t), π'b = G * B(t) * kb
πc = G * C(t), π'c = G * C(t) * k_c

Note that the prover does not actually need to know (and should not know!) t, ka, kb, or k_c to compute these values; rather, the prover should be able to compute these values solely based on the points we added to the trusted setup.

The next step is to ensure that all three linear combinations have the same coefficients. We can do this by adding another set of values to the trusted setup: G * (Ai(t) + Bi(t) + C_i(t)) * b, where b is another number that should be considered "toxic waste" and is discarded immediately after the trusted setup is completed. Then, we can have the prover create a linear combination using these values with the same coefficients and use the same pairing technique as above to verify that this value matches the provided A + B + C.

Finally, we need to prove that A * B - C = H * Z. We perform this again using a pairing check:

e(πa, πb) / e(πc, G) ?= e(πh, G * Z(t))

where π_h = G * H(t). If the connection between this equation and A * B - C = H * Z does not make sense to you, please go back and read the article on pairings.

We have seen above how to convert A, B, and C into elliptic curve points; G is just a generator (i.e., the elliptic curve point equivalent of the number one). We can add G * Z(t) to the trusted setup. H is harder; H is just a polynomial, and we rarely predict the coefficients of each individual QAP solution in advance. Therefore, we need to add more data to the trusted setup; specifically, the sequence:

G, G * t, G * t², G * t³, G * t⁴ … .

In the Zcash trusted setup, this sequence goes up to about 2 million; this is how many powers you need to ensure that you can always compute H(t), at least for the specific QAP instances they care about. This way, the prover can provide all the information to the verifier for the final check.

There is one more detail we need to discuss. Most of the time, we do not just want to abstractly prove that a solution to some specific problem exists; rather, we want to prove the correctness of a specific solution (for example, proving that if you use the word "cow" and hash it with SHA3 a million times, the final result starts with 0x73064fe5), or if you restrict the solution to some parameters. For example, in cryptocurrency instances where transaction amounts and account balances are encrypted, you want to prove that you know some decryption key k such that:

The encrypted oldbalance, txvalue, and new_balance should be publicly specified, as these are the specific values we want to verify at a specific time; only the decryption key should be hidden. Some subtle modifications to the protocol are needed to create a "custom verification key" corresponding to certain specific constraints of the input.

Now, let’s take a step back. First, here is the complete verification algorithm provided by Ben Sasson, Tromer, Virza, and Chiesa:

The first line handles parameterization; essentially, you can think of its function as creating a "custom verification key" for a specific instance of a problem that specifies certain parameters. The second line checks the linear combinations of A, B, and C; the third line checks whether the linear combinations have the same coefficients, and the fourth line is the product check A * B - C = H * Z.

In summary, the verification process consists of several elliptic curve multiplications (one for each "public" input variable) and five pairing checks, one of which includes an additional pairing multiplication. The proof contains eight elliptic curve points: A(t), B(t), and C(t) each have a pair of points, b * (A(t) + B(t) + C(t)) has a point πk, and there is a point πh for H(t). Seven of these points are on the curve Fp (each 32 bytes, since you can compress the y-coordinate to a bit), while in the Zcash implementation, one point (πb) is on the twisted curve F_p² (64 bytes), so the total size of the proof is about 288 bytes.

The two computationally hardest parts of creating the proof are:

Dividing (A * B - C) / Z to obtain H (an algorithm based on fast Fast Fourier Transform can accomplish this in sub-quadratic time, but it is still computationally intensive)
Performing elliptic curve multiplication and addition operations to create A(t), B(t), C(t), and H(t) values and their corresponding pairs
The fundamental reason why creating the proof is so difficult is that if we are to make a zero-knowledge proof from it, a single binary logic gate in the original computation turns into operations that must be encrypted through elliptic curve operations. This fact, combined with the superlinear nature of the Fast Fourier Transform, means that creating proofs for Zcash transactions takes about 20-40 seconds.

Another very important question is: can we try to make the trusted setup slightly… less trusted? Unfortunately, we cannot make it completely trustless; the KoE assumption itself excludes the possibility of creating independent pairs (Pi, Pi * k) without knowing what k is. However, we can significantly enhance security by using N-of-N multiparty computation—that is, building a trusted setup among N parties, as long as at least one participant deletes their toxic waste, then you are good.

To give you a glimpse of how to perform this, here is a simple algorithm for taking an existing set (G, G * t, G * t², G * t³…) and "adding" your own secret so that you need both your secret and the previous secret (or a previous set of secrets) to cheat.

The output set is quite simple:

G, (G * t) * s, (G * t²) * s², (G * t³) * s³…

Note that you can generate this set by only knowing the original set and s, and the functionality of the new set is the same as the old set, except now using t * s as "toxic waste" instead of t. As long as you and the person (or people) who created the previous set have not deleted your toxic waste and subsequently colluded, the group is "secure."

Doing this for a complete trusted setup is much more difficult because it involves multiple values and must be completed in several rounds among the parties. This is an actively researched area to see if multiparty computation algorithms can be further simplified and require fewer rounds or be more parallelizable, as the more you can do, the more participants can be involved in the trusted setup process. It is reasonable to see why a trusted setup among six participants who know each other and work together might make some people uncomfortable, but a trusted setup with thousands of participants is almost indistinguishable from being completely untrusted—and if you are really paranoid, you can enter and participate in the setup process yourself and ensure that you personally delete your values.

Another active area of research is to achieve the same goals using other methods that do not use pairings and the same trusted setup paradigm. See Eli Ben Sasson's recent presentation for another option (though note that it is at least as mathematically complex as SNARKs!).

Special thanks to Ariel Gabizon and Christian Reitwiessner for their review.