IOSG: Why are we optimistic about hardware acceleration for zero-knowledge proofs?

Author: Bryan, IOSG Ventures

This article will mainly discuss the current development status of ZKP as a scaling solution, describing several dimensions that need to be optimized in the proof generation process from a theoretical perspective, and delving into the demand for acceleration in different scaling solutions. Then, it will focus on hardware solutions, looking forward to the Moore's Law in the field of zk hardware acceleration. Finally, some opportunities and current situations in the hardware zk acceleration field will be elaborated at the end of the article. First, there are three main dimensions that affect proof speed: proof systems, the scale of the circuit to be proven, and algorithmic hardware and software optimization.

For proof systems, any algorithm that uses elliptic curves (EC), such as the mainstream zk-snark algorithms like Groth 16 (Zcash), Galo2 (Scroll), and Plonk (Aztec, Zksync), has a bottleneck in the process of generating polynomial commitments involving large scalar multiplication (MSM), which currently has a long time (high computational requirements). For FRI-based algorithms, such as ZK-Stark, the method of generating polynomial commitments is through Hash Functions, which do not involve EC, thus not involving MSM calculations.

The proof system is fundamental, and the scale of the circuit to be proven is also one of the core hardware optimization needs. The recently discussed ZKEVM has different levels of compatibility with Ethereum, leading to varying circuit complexities. For example, Zksync/Starkware has built a virtual machine that differs from native Ethereum, thus bypassing some of the underlying code that is not suitable for zk processing, reducing the complexity of the circuit, while Scroll/Hermez, aiming for bottom-level compatibility with zkEVM, naturally has a more complex circuit.

A convenient analogy is that the complexity of the circuit can be understood as the number of seats on a bus. For ordinary days, the number of passengers to be carried is below 30, and some buses have chosen 30 seats, which are Zksync/StarkWare. However, there are some days in a year with particularly many passengers, and ordinary buses cannot accommodate them, so some buses are designed with more seats (Scroll). But these days may be relatively few, leading to many empty seats on regular days.

Hardware acceleration is more urgent for these more complex circuit designs, but this is more of a spectrum issue, and it is equally beneficial and detrimental for ZKEVM.

Different proof system optimization needs/focus:

Basic:

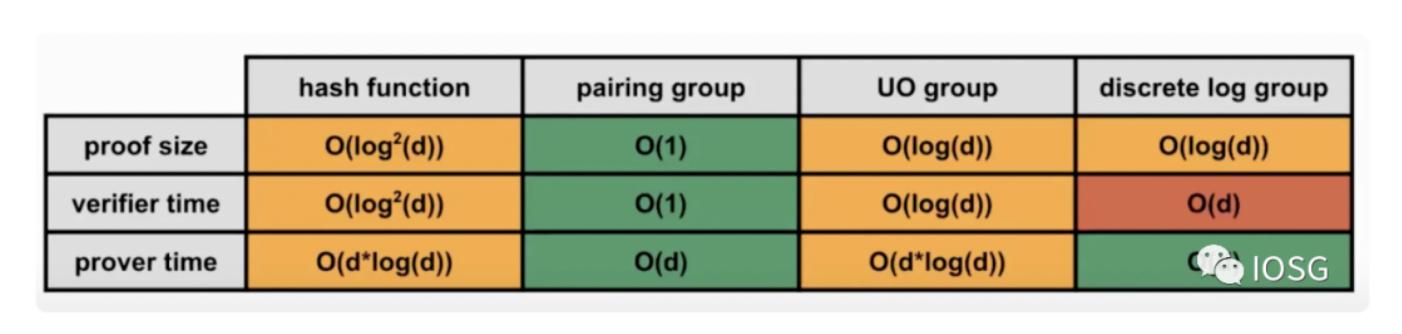
When a thing to be proven is processed through a circuit (such as R1CS/QAP), a set of scalars and vectors will be obtained, which are then used to generate polynomials or other forms of algebraic forms such as inner product arguments (groth16). This polynomial is still quite lengthy, and if proof is generated directly, both the proof size and verification time will be large. Therefore, we need to further simplify this polynomial. The optimization method here is called polynomial commitment, which can be understood as a special hash value of the polynomial. Algebra-based polynomial commitments include KZG, IPA, DARK, all of which use elliptic curves to generate commitments.

FRI is the main method for generating commitments based on Hash Functions. The choice of polynomial commitment mainly revolves around a few points - security and performance. Security here mainly considers the setup phase. If the randomness used to generate the secret is public, such as FRI, then we say this setup is transparent. If the randomness used to generate the secret is private and needs to be destroyed after use by the Prover, then this setup needs to be trusted. MPC is a means to solve the trust issue here, but in practical applications, it has been found that this requires users to bear certain costs.

However, the aforementioned FRI, which is relatively excellent in terms of security, does not perform well in terms of performance. Meanwhile, although pairing-friendly elliptic curves have excellent performance, when considering the addition of recursion, there are not many suitable curves, so there is also considerable overhead.

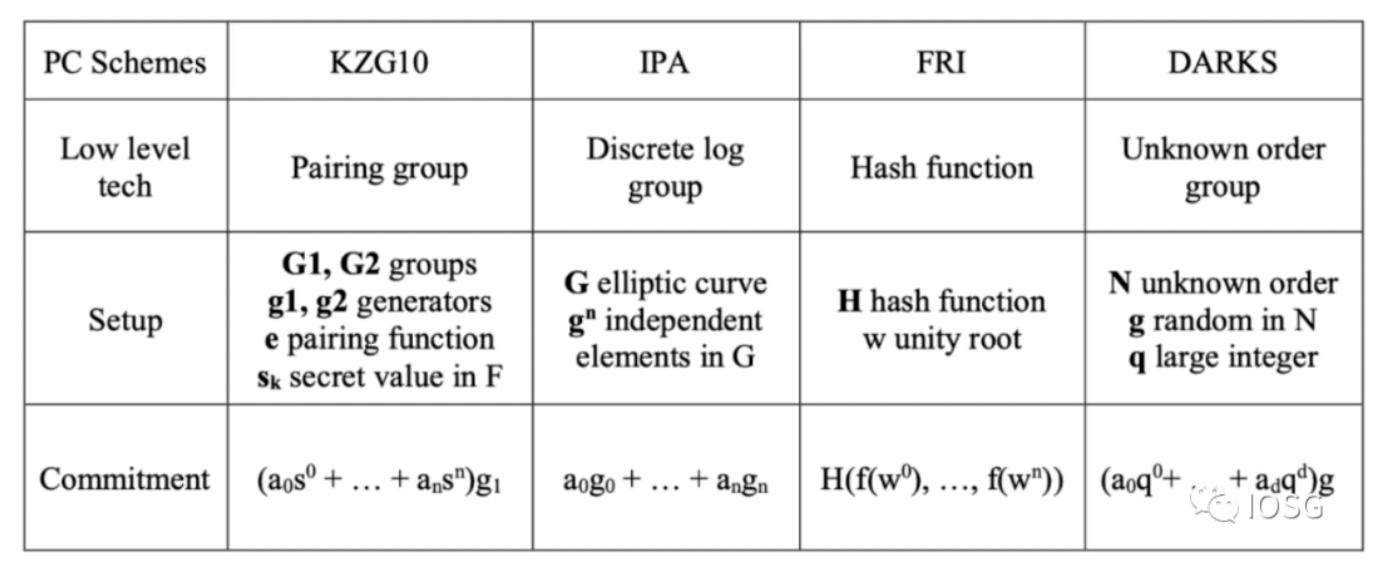Image source: https://hackernoon.com

Justin Drake on Polynomial commitment, Part 1

Industry Status:

Currently, whether based on Plonk (matterlabs) or Ultra-Plonk (Scroll, PSE), their final polynomial commitment is based on KZG, so most of the work of the Prover will involve a large amount of FFT calculations (to generate polynomials) and ECC point multiplication MSM calculations (to generate polynomial commitments).

In pure Plonk mode, since the number of points to be committed is not large, the proportion of Prove time occupied by MSM calculations is not high, so optimizing FFT performance can bring greater performance improvements in the short term. However, in the UltraPlonk (halo2) framework, due to the introduction of customer gates, the number of points committed in the prover phase increases, making the performance optimization of MSM calculations very important. (Currently, after Pippenger optimization of MSM calculations, it still requires log(P(logB)) (B is the upper bound of exp, p is the number of points participating in MSM).

Currently, the new generation Plonky2 proof system uses FRI, which is common in the STARK system, instead of KZG for polynomial commitment, allowing Plonky2's prover to no longer consider MSM, thus theoretically, the performance improvement of this system no longer relies on MSM-related algorithm optimization. The author of Plonky2, Mir (currently at Polygon Zero), is actively promoting this system. However, since the Goldilocks Field used in Plonky2 is not particularly friendly for writing circuits related to elliptic hash algorithms (such as ECDSA), it is still difficult to determine whether Mir or the PSE/Scroll solution is better.

Based on a comprehensive consideration of the Prove algorithms of Plonk, Ultraplonk, and Plonky2, the modules that need hardware acceleration will likely still focus on FFT, MSM, and HASH.

Another bottleneck for the Prover is the generation of witnesses. Typically, ordinary non-zk calculations omit a large number of intermediate variables, but in the ZK proof process, all witnesses need to be recorded and will participate in subsequent FFT calculations, so how to efficiently parallelize witness calculations will also be a potential consideration for the Prover's mining machine.

Attempts to accelerate ZKP: recursive proof - The fractal L3 concept of StarkNet is based on the concept of recursive proof, Zksync's fractal hyperscaling, and Scroll also has similar optimizations.

The concept of Recursive zkSNARK is to prove the verification process of a Proof A, thereby generating another Proof B. As long as the Verifier can accept B, it is equivalent to accepting A. Recursive SNARK can also aggregate multiple proofs together, such as aggregating the verification processes of A1, A2, A3, and A4 into B; recursive SNARK can also break down a long computation process into several steps, where each step's computation proof S1 must be verified in the next step's computation proof, i.e., compute one step, verify one step, then compute the next step, allowing the Verifier to only need to verify the last step, thus avoiding the difficulty of constructing an indefinitely long circuit.

Theoretically, zkSNARK supports recursion, some zkSNARK solutions can directly implement the Verifier using circuits, while others need to split the Verifier algorithm into parts that are easy to circuit and parts that are not easy to circuit, the latter adopting a delayed aggregation verification strategy, placing the verification process at the last step of the verification process.

In the future applications of L2, the advantages of recursion can further reduce costs and performance requirements through the induction of things to be proven.

The first scenario (application-agnostic) is for different things to be proven, such as one being a state update and the other being a Merkle Tree. The proofs of these two things can be combined into one proof but still have two output results (used for verifying public keys separately).

The second scenario (applicative recursion) is for similar things to be proven, such as two state updates. In this case, these two things can be aggregated before generating the proof, resulting in only one output, which is the state difference after two updates. (Zksync's method is also similar, where user costs are only responsible for the state difference.)

In addition to recursive proof and the hardware acceleration mainly discussed below, there are other ways to accelerate ZKP, such as custom gates, removing FFT (the theoretical basis of OlaVM), etc., but this article will not discuss them due to space limitations.

Hardware Acceleration

Hardware acceleration has always been a common way to accelerate cryptographic proofs, whether for RSA (the underlying mathematical logic of RSA is similar to that of elliptic curves, also involving many complex large number calculations) or early GPU-based optimizations for zk-snark in zcash/filecoin.

Hardware Choices

After the Ethereum The Merge, there will inevitably be a large amount of GPU computing power redundancy (partly affected by the change in Ethereum's consensus, with GPU giant Nvidia's stock price dropping by 50% since the beginning of the year, while inventory redundancy is also continuously increasing). The following chart shows the transaction price of Nvidia's flagship GPU RTX 3090, indicating that buyer power is relatively weak.

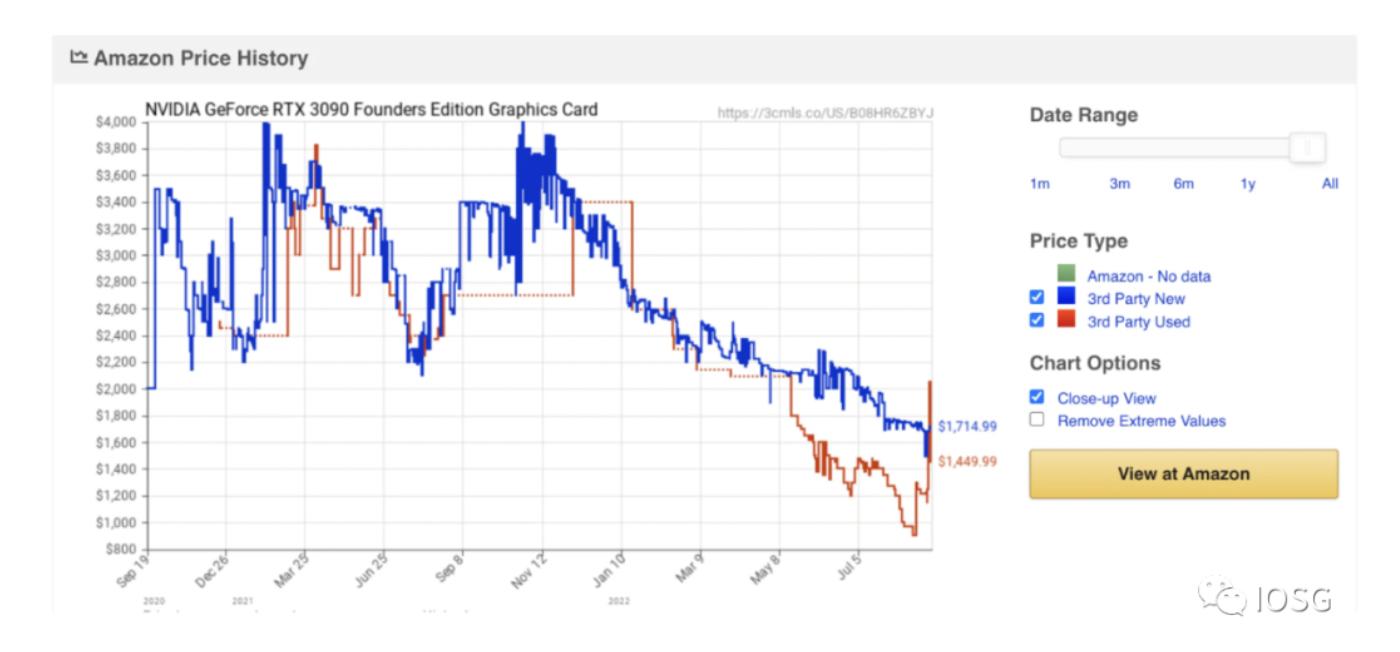
With GPU prices at a low point and a large amount of GPU computing power idle, a natural question arises: is GPU suitable hardware for accelerating zk? There are mainly three hardware options: GPU/FPGA/ASIC.

FPGA vs GPU:

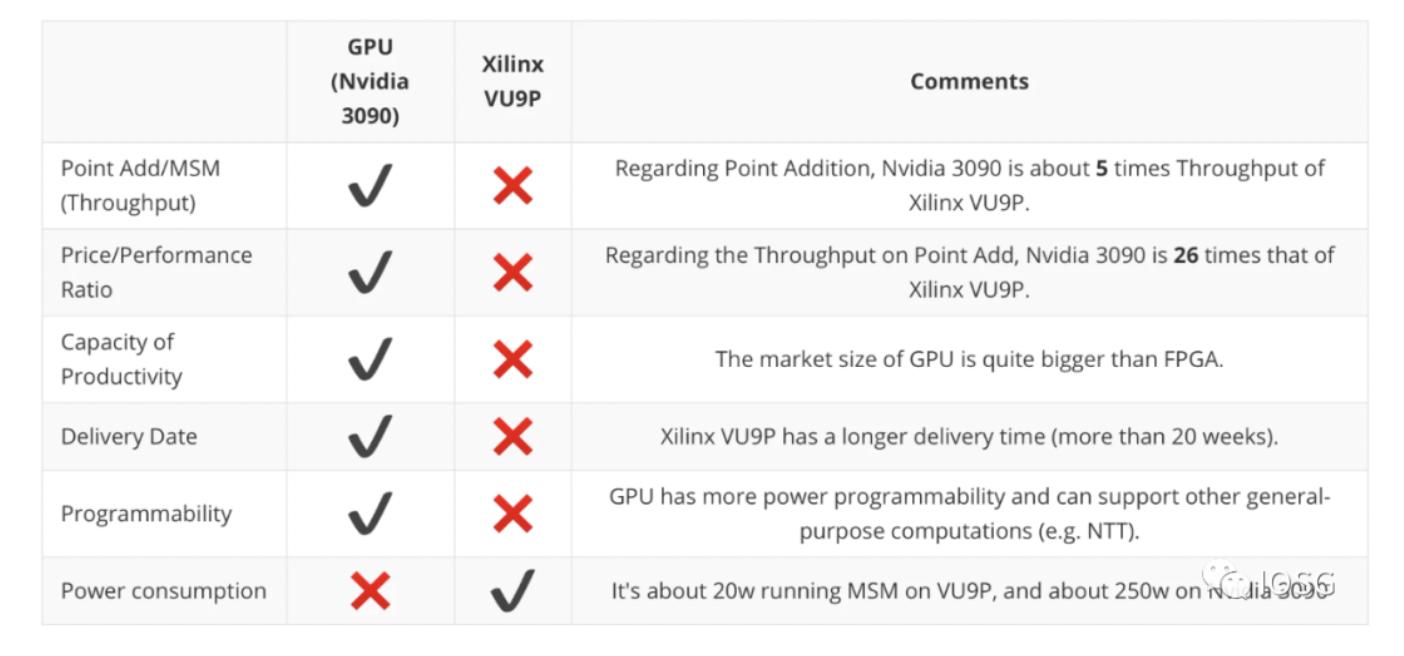
First, a summary: Below is a summary by trapdoor-tech comparing GPU (using Nvidia 3090 as an example) and FPGA (using Xilinx VU9P as an example) across several dimensions. A very important point is that GPUs outperform FPGAs in performance (speed of proof generation), while FPGAs have advantages in energy consumption.

A more intuitive specific running result from Ingoyama:

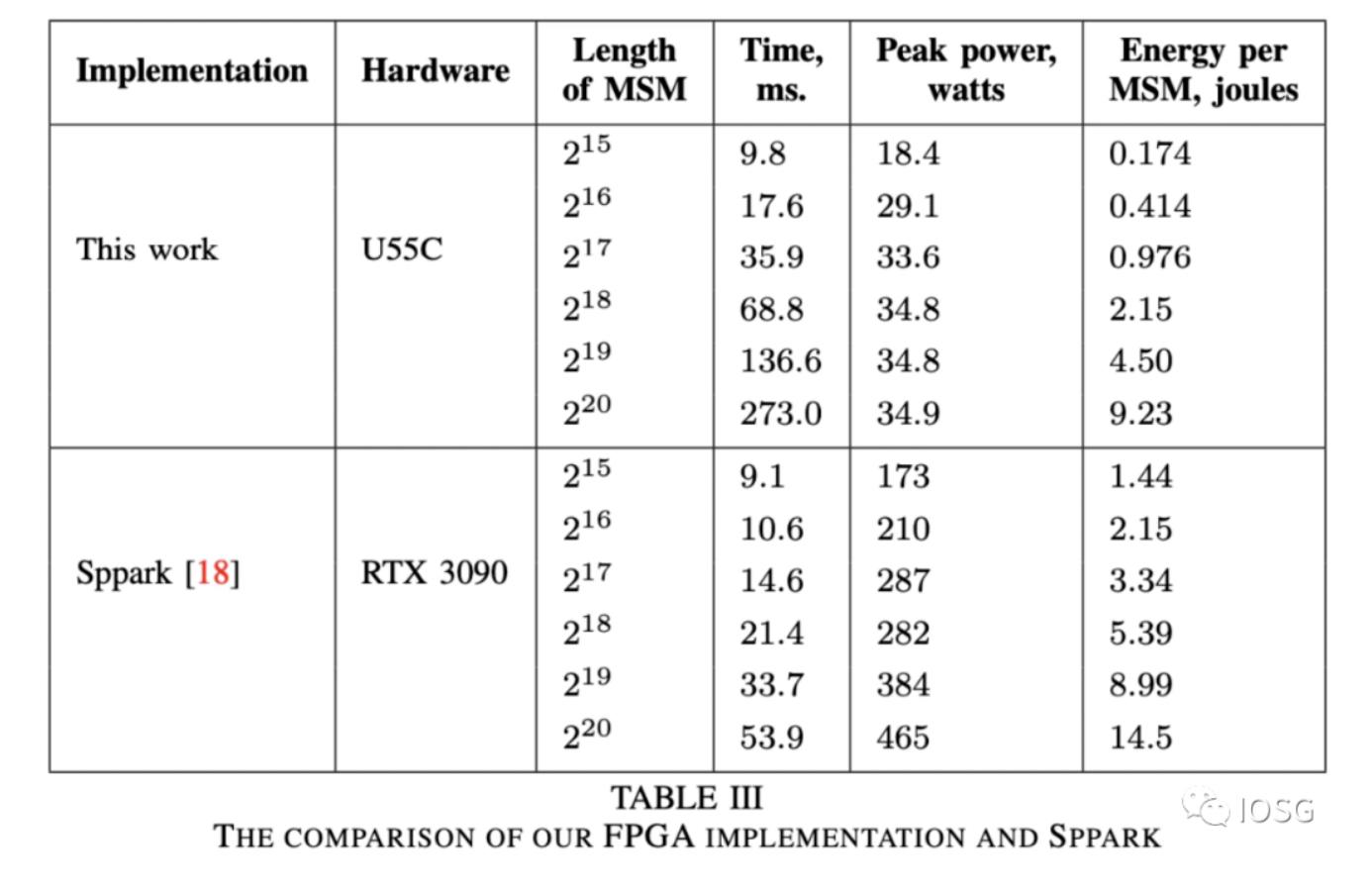
Especially for operations with higher bit widths (2^20), GPUs are five times faster than FPGA operations, while consuming much more power.

For ordinary miners, cost-effectiveness is also an important factor in deciding which hardware to use. Whether U55C ($4795) or VU9P ($8394), the prices are much higher compared to GPU (RTX 3090: $1860).

Theoretically, GPUs are suitable for parallel computing, while FPGAs pursue programmability. However, these advantages do not perfectly apply in the environment of zero-knowledge proof generation. For example, the parallel computing suitable for GPUs is for large-scale graphics processing, and although it is logically similar to MSM processing, the applicable range (floating number) is not consistent with the specific finite fields targeted by zkps. For FPGAs, programmability in the application scenarios of multiple L2s is not clear, as considering that L2 miner rewards are linked to the needs of a single L2 (unlike pow), there is a low likelihood of a winner-takes-all situation in niche tracks, leading to infrequent changes in algorithms for miners.

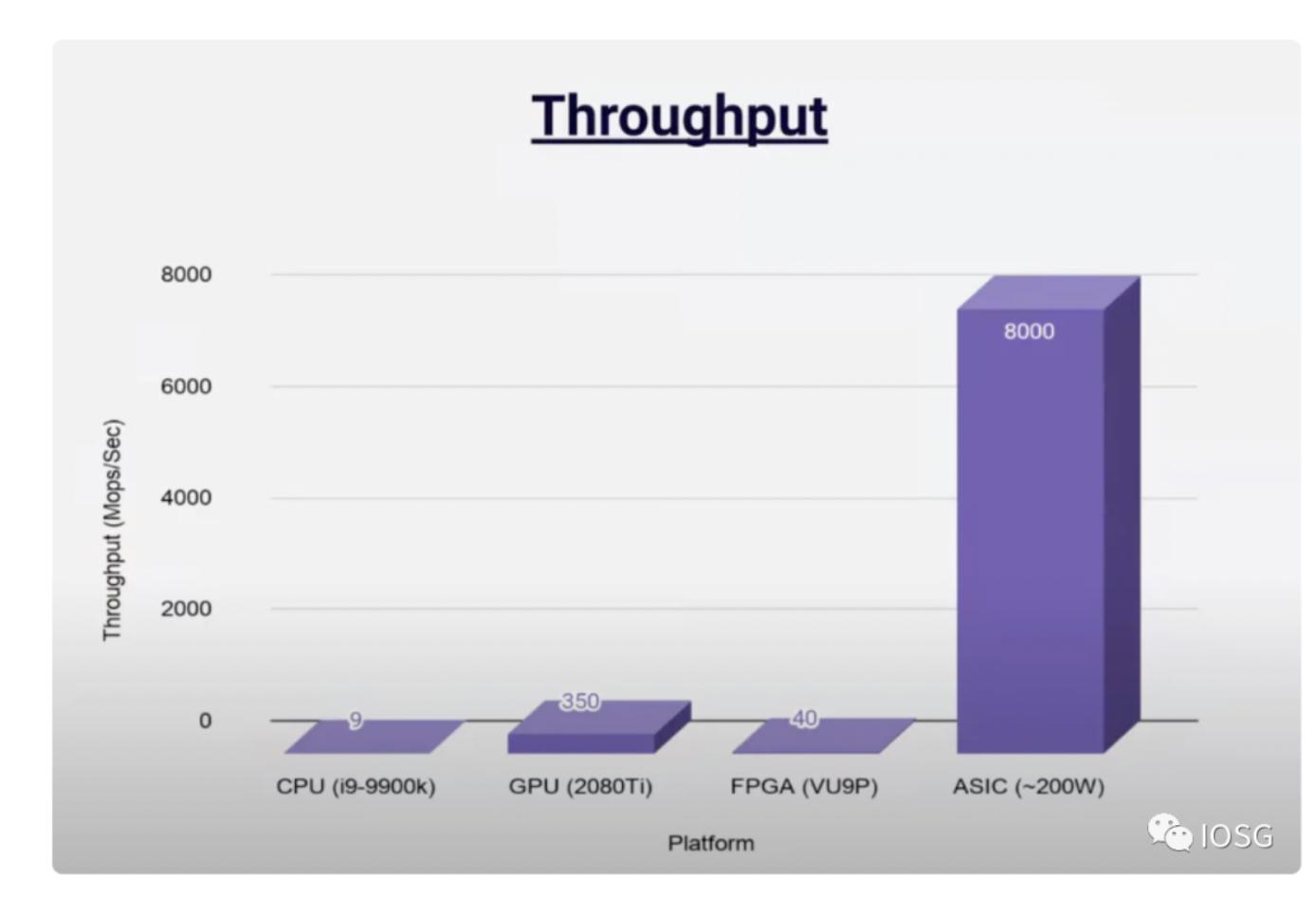ASIC is a solution that balances performance and cost (including throughput, latency, etc.), but whether it is the best solution is still inconclusive. The issues it faces are:

Long development time - it requires going through the entire process from chip design to chip production. Even if the chip has been designed, chip production is a lengthy, costly process with varying yields. In terms of foundry resources, TSMC and Samsung are the best chip foundries, and currently, TSMC's orders are booked for two years ahead. Competing for foundry resources with ZK chips are AI chips and electric vehicle chips, which are already proven products with early chip designs in web2, while the demand for ZK chips is not clear.

Secondly, the performance of the entire chip is inversely related to the size of a single chip, meaning that the smaller the single chip, the more chips can be accommodated on the wafer, thus increasing overall performance. Currently, the technology for manufacturing high-end chips is monopolized (for example, photolithography technology, the most complex part of chip manufacturing, is monopolized by the Dutch company ASML). For some small and medium-sized foundries (such as China's SMIC), being one or two generations behind the top technology means they lag behind the best foundries in terms of yield and chip size. This will lead to ZK chips only being able to seek some suboptimal solutions, and of course, based on cost considerations in a situation where demand is not so clear, choosing non-high-end chips around 28nm.

Currently, the main ASIC solutions are focused on FFT and MSM, two common operators with high computational demands in ZK circuits, and are not designed for specific projects, so the efficiency of specific operations is not theoretically the highest. For example, the logical circuit of Scroll's prover has not yet been fully realized, so there is naturally no corresponding hardware circuit that matches it. Moreover, ASICs are application-specific and do not support subsequent adjustments. When the logical circuit changes, such as when the node's client needs to upgrade, it is uncertain whether there is a solution that can also be compatible.

At the same time, the lack of talent is also a current industry situation for ZK chips. It is not easy to find talent who understands both cryptography and hardware, and suitable candidates need to have a deep mathematical background as well as years of experience in hardware product design and maintenance.

Closing thoughts - Prover Development Trend EigenDA

The above are the industry's thoughts and attempts to accelerate ZKP, ultimately meaning that the threshold for running provers will become lower and lower. Periodically, provers need to go through roughly the following three phases:

Phase I: Cloud-based Prover

Cloud-based provers can significantly lower the entry threshold for third-party provers (non-users/project parties), similar to web2's AWS/Google Cloud. From a business model perspective, project parties will lose a portion of rewards, but from a decentralization narrative, this is a way to attract more participants economically and operationally. Cloud computing/cloud services are existing technologies in the web2 stack, with mature development environments available for developers, and can leverage the unique low threshold/high clustering effect of the cloud, making it a choice for short-term proof outsourcing.

Currently, Ingoyama has also implemented this (the latest F1 version even reached twice the benchmark speed of pipeMSM). However, this is still a method where a single prover runs the entire proof, while in Phase II, proofs can exist in a decomposable form, with more participants involved.

Phase II: Prover Marketplace

The proof generation process involves different computations, some of which prefer efficiency, while others have requirements for cost/energy consumption. For example, MSM calculations involve pre-computation, which requires certain memory to support different scalar granules on pre-computation. If all scalars exist on one computer, the memory requirements for that computer will be high. However, if different scalars are stored on multiple servers, not only will the speed of such calculations improve, but the number of participants will also increase.

The marketplace is a bold thought in terms of business models for the aforementioned outsourced calculations. However, there are precedents in the crypto space - Chainlink's oracle service, where price feeds for different trading pairs on different chains also exist in a marketplace format. At the same time, Aleo's founder Howard Wu once co-authored a paper on DIZK, a methodology for generating zero-knowledge proofs for distributed ledgers, which is theoretically feasible.

That said, from a business model perspective, this is a very interesting thought, but there may also be significant execution difficulties in practical implementation, such as how to coordinate these calculations to generate a complete proof, which must not lag behind Phase I in terms of time and cost.

Phase III: Everyone Runs Prover

In the future, Provers will run on users' local devices (web or mobile), as Zprize has competitions and rewards related to ZKP acceleration based on webassembly/android execution environments, meaning that to some extent, users' privacy will be ensured (current centralized provers are only for scaling and do not guarantee user privacy). Most importantly, the privacy here is not limited to on-chain behavior but also includes off-chain behavior.

One must consider the issue of security on the web side, as the execution environment on the web has higher prerequisites for security compared to hardware (an industry witness is that web wallets like Metamask are less secure than hardware wallets).

In addition to on-chain data proofs off-chain, uploading off-chain data to on-chain in the form of ZKP while fully protecting user privacy can only be established in this phase. Current solutions inevitably face two problems - 1. Centralization, meaning that users' information still carries the risk of being censored; 2. The verifiable data forms are singular. Because off-chain data is diverse and unstandardized, verifiable data forms require extensive cleaning/screening, while still being singular in form.

The challenges here are not just in the proof generation environment; whether there are algorithms that can be compatible (first must use transparent algorithms), as well as cost/time/efficiency, all need to be considered. However, the demand is also unparalleled; imagine being able to collateralize real-life credit on-chain in a decentralized manner for lending, without the risk of censorship.