Vitalik's New Work: Incomplete Guide to Stealth Addresses

Original Title: An incomplete guide to stealth addresses
Author: Vitalik Buterin
Compiled by: Karen, Foresight News

One of the biggest challenges in the current Ethereum ecosystem is privacy. By default, anything that enters a public blockchain is public, which means not only assets and transaction activities but also ENS domain names, POAPs, NFTs, and soulbound tokens. Using a range of Ethereum applications means that many of your activities are open for anyone else to view and analyze.

We need to improve this situation. However, so far, discussions about improving privacy have mainly revolved around a specific use case: privacy-preserving transfers of ETH and mainstream ERC20 tokens. This article will describe a different category of tools, mechanisms, and use cases that can improve the privacy status of Ethereum in many other scenarios, namely the concept of "stealth addresses."

What is a stealth address system?

Suppose Alice wants to transfer assets to Bob, which could be a certain amount of cryptocurrency (e.g., 1 ETH, 500 RAI) or an NFT. When Bob receives the assets, he does not want others to know that he is the recipient. It is impossible to hide the fact that a transfer has occurred, especially if the transfer involves an NFT that exists only as a single copy on-chain, but hiding who the recipient is may be more feasible.

What Alice and Bob would prefer is a payment flow system where Bob sends Alice (or an ENS domain) some "address" encoding that can receive payments; this information alone is sufficient for Alice (or anyone else) to send him assets, and it is almost identical to the current payment workflow.

It is important to note that this privacy is entirely different from the privacy provided by Tornado Cash. Tornado Cash can hide transfers of mainstream fungible assets like ETH or major ERC-20 tokens (often used for privately sending to oneself), but it is very weak in adding privacy for lesser-known ERC20 transfers and cannot add privacy for NFT transfers at all.

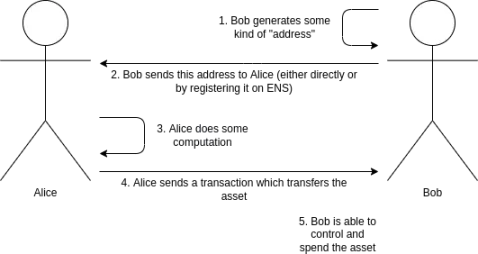
As mentioned above, the typical workflow for making payments with cryptocurrency adds privacy, meaning that no one can know that the asset recipient is Bob, and the workflow remains unchanged.

A stealth address is an address that can be generated by either Alice or Bob but can only be controlled by Bob. Bob generates a spending key and keeps it secret, then uses that key to generate a stealth meta-address. He passes this meta-address to Alice (or registers it on ENS). Alice can perform calculations on this meta-address to generate a stealth address that belongs to Bob. Alice can then send any assets she wants to this address, and Bob will have complete control over those assets. During the transfer, Alice publishes some additional cryptographic data (a temporary public key) on-chain to help Bob discover that this address belongs to him.

Another way to look at it is that stealth addresses provide the same privacy properties for Bob by generating a new address for each transaction without requiring any interaction from Bob.

The complete workflow of the stealth address scheme is as follows:

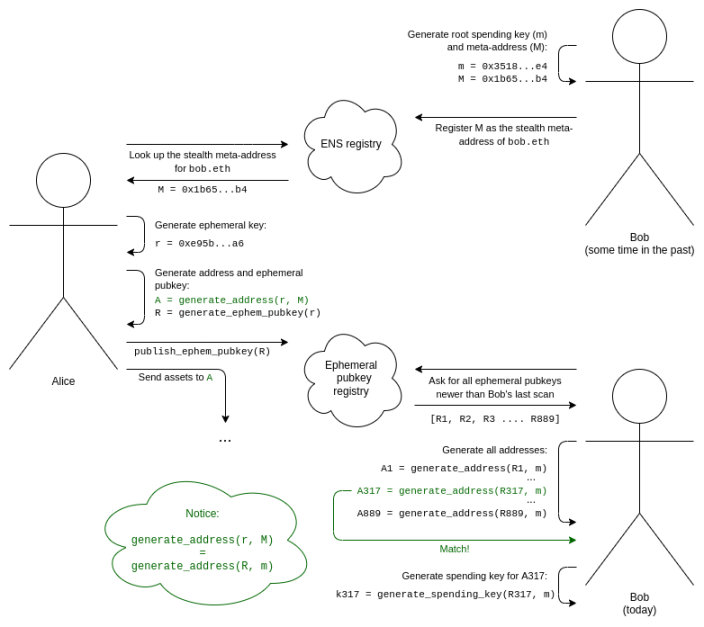
1. Bob generates his root spending key (m) and stealth meta-address (M).

2. Bob adds an ENS record to register (M) as the stealth meta-address bob.eth.

3. We assume Alice knows Bob's address is bob.eth. Alice looks up Bob's stealth meta-address (M) on ENS.

4. Alice generates a temporary key (r) that only she knows and can use only once (to generate this specific stealth address).

5. Alice uses an algorithm to combine her temporary key and Bob's meta-address to generate a stealth address. She can now send assets to this address.

6. Alice also generates her temporary public key and publishes it to the temporary public key registry (this can be done in the same transaction as the first transaction sending assets to this stealth address).

7. For Bob to discover the stealth address that belongs to him, he needs to scan the temporary public key registry to look for the entire list of temporary public keys published by anyone since his last scan.

8. For each temporary public key, Bob tries to combine it with his root spending key to generate a stealth address and checks if there are any assets in that address. If there are, Bob calculates the spending key for that address and remembers it.

All of this relies on two uses of cryptographic deception. First, we need a pair of algorithms to generate a shared secret: one algorithm uses Alice's temporary key and Bob's meta-address, while the other uses Bob's root spending key and Alice's temporary public key. This can be accomplished in various ways; Diffie-Hellman key exchange is one of the achievements of modern cryptography that happens to accomplish this.

However, merely sharing a secret is not enough: if we simply generate a private key from the shared secret, then both Alice and Bob could spend from that address. We also add a key blinding mechanism: in a pair of algorithms, Bob can combine the shared key with his root spending key, while Alice can combine the shared key with Bob's meta-address, allowing Alice to generate the stealth address and Bob to generate the spending key for that stealth address, all without creating a public link between the stealth address and Bob's meta-address (or between one stealth address and another).

Hiding addresses using elliptic curve cryptography

The use of elliptic curve cryptography to hide addresses was initially introduced by Peter Todd in 2014 in the context of Bitcoin. The technology works as follows:

• Bob generates a key (m) and computes M = G * m, where G is the recognized generator point of the elliptic curve. The stealth meta-address is (M).

• Alice generates a temporary key (r) and publishes the temporary public key R = G * r.

• Alice can compute a shared key S = M * r, and Bob can also compute the same shared key S = m * R.

• Generally, in Bitcoin and Ethereum (including correctly designed ERC-4337 accounts), addresses are hashes that contain public keys used to verify transactions from that address. Therefore, if you compute the public key, you can compute the address. To compute the public key, either Alice or Bob can compute P = M + G * hash(S).

• To compute the private key for that address, Bob can compute p = m + hash(S).

This satisfies all of our requirements above and is very simple.

There is even an EIP attempting to define a stealth address standard for Ethereum that supports this method while also allowing users to develop other methods (for example, supporting Bob having separate spending and viewing keys or using different cryptography for quantum resistance). Now you might think: stealth addresses are not that difficult; the theoretical knowledge is solid, and adoption is merely an implementation detail. However, the problem is that a truly effective implementation requires addressing some important implementation details.

Stealth addresses and paying transaction fees

Suppose someone sends you an NFT. If you want to ensure privacy, they will send it to a stealth address that you control. After scanning the temporary public key on-chain, your wallet will automatically discover that address. You can now freely prove ownership of the NFT or transfer it to others. But there is a problem: the ETH balance in that account is 0, so you cannot pay transaction fees. Even ERC-4337 token payers will not work, as they only apply to fungible ERC20 tokens. Moreover, you cannot send ETH from your main wallet to it, as that would create a publicly visible link, meaning you lose privacy.

One simple way to solve this problem is to use ZK-SNARKs to transfer funds to pay for fees. But this would consume a lot of Gas, with a single transfer potentially consuming hundreds of thousands of Gas.

A more clever approach involves trusting specialized transaction aggregators (searchers in MEV terminology). These aggregators would allow users to pay once to purchase a set of "tickets" that can be used to pay for on-chain transactions. When a user needs to spend an NFT in a stealth address that contains nothing else, they provide one of the tickets to the aggregator, encoded using Chaumian blinding. This is the original protocol used in centralized privacy-preserving electronic cash schemes proposed in the 1980s and 1990s. The searchers accept the ticket and repeatedly include the transaction for free in their bundles until the transaction is successfully accepted in a block.

Stealth addresses and separating spending and viewing keys

Suppose Bob does not want just one main "root spending key" that can do everything, but instead wants a separate root spending key and viewing key. The viewing key can see all of Bob's stealth addresses but cannot spend.

In the elliptic curve world, this can be solved using a very simple cryptographic trick:

• Bob's meta-address (M) now takes the form of (K, V), encoding G * k and G * v, where k is the spending key and v is the viewing key.

• The shared key is now S = V * r = v * R, where r is still Alice's temporary key and R is still the temporary public key published by Alice.

• The public key of the stealth address is P = K + G * hash(S), and the private key is p = k + hash(S).

The first step (generating the shared secret) uses the viewing key, while the second step (the parallel algorithms for Alice and Bob to generate the stealth address and its private key) uses the root spending key.

This has many use cases. For example, if Bob wants to receive POAPs, he can give his POAP wallet (or even a less secure web interface) the viewing key to scan the chain and see all his POAPs without giving that interface the power to spend those POAPs.

Stealth addresses and easy scanning

To make it easier to scan the entire set of temporary public keys, one technique is to add a view tag to each temporary public key. One way to implement this in the above mechanism is to make the view tag one byte of the shared key (for example, the x-coordinate of S modulo 256, or the first byte of hash(S)).

This way, Bob only needs to perform elliptic curve multiplication once for each temporary public key to compute the shared key, and the view tag makes scanning easier.

Stealth addresses and quantum resistance

The above scheme relies on elliptic curves, but while this scheme works well, unfortunately, it is vulnerable to attacks from quantum computers. We will need to switch to quantum-resistant algorithms. There are two natural candidates: isogenies and lattices.

Isogenies are a very different mathematically based construction that has linear properties, allowing us to use cryptographic tricks similar to what we did above while cleverly avoiding constructing cyclic groups that may be vulnerable to quantum computer discrete logarithm attacks.

The main weakness of isogeny-based cryptography is its highly complex underlying mathematics and the risk of hiding potential attacks under this complexity. Some isogeny-based protocols were attacked last year, but other protocols remain secure. The main advantage of isogenies is their relatively small key sizes and the ability to directly transplant various elliptic curve methods.

A 3-isogeny in CSIDH

Lattices are a very different cryptographic structure that relies on simpler mathematics than isogenies and can do some very powerful things (such as fully homomorphic encryption). Stealth address schemes can be built on lattices, although designing the best scheme is an open question. However, lattice-based structures often have larger key sizes.

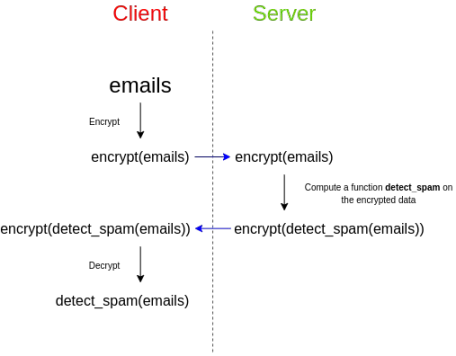
Fully homomorphic encryption, applications of lattices. FHE can also help stealth address protocols in different ways: helping Bob outsource the computation of whether a stealth address contains assets across the entire chain without revealing his viewing key.

A third approach is to build stealth address schemes from general-purpose black-box primitives. The shared key generation part of this scheme directly maps to key exchange, which is an important component of public key encryption systems. The harder part is to get Alice to generate only the stealth address (not the spending key) and to have Bob generate the spending key through a parallel algorithm.

Unfortunately, you cannot use simpler components than those required to build a public key encryption system to construct stealth addresses. A simple proof is that you can build a public key encryption system from a stealth address scheme. If Alice wants to encrypt a message for Bob, she can send N transactions, each either to one of Bob's stealth addresses or to one of her own stealth addresses, and Bob can see which transactions he received to read the message. This is important because in a mathematical proof, you cannot just use hashes to do public key encryption, while you can use hashes to do zero-knowledge proofs, so stealth addresses cannot be accomplished with hashes alone.

This is indeed a method using relatively simple components: zero-knowledge proofs, which can consist of hashes and (key-hiding) public key encryption. Bob's meta-address is a public encryption key plus a hash h = hash(x), and his spending key is the corresponding decryption key plus x. To create a stealth address, Alice generates a value c and publishes the Bob-readable c encrypted as her temporary public key. The address itself is an ERC-4337 account, whose code verifies transactions by requiring zero-knowledge proofs that demonstrate ownership of values x and c, making k = hash(hash(x), c) (where k is part of the account code). Knowing x and c, Bob can reconstruct the address and code himself.

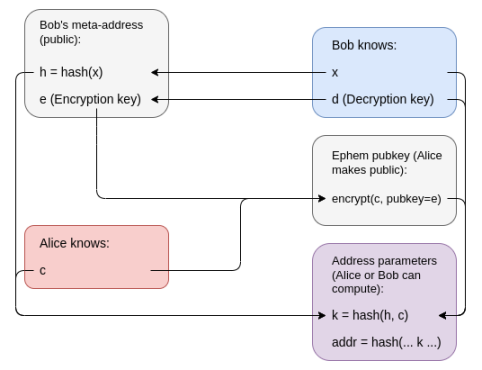
The encryption of (c) does not reveal any information to anyone other than Bob, and (k) is a hash that reveals almost nothing about c. The wallet code itself only contains (k), and the privacy of (c) means that (k) cannot be traced back to (h).

However, this requires a STARK. Ultimately, I believe that the post-quantum Ethereum world will likely involve applications using many STARKs, so I advocate for aggregation protocols as described here to combine all these STARKs into a recursive STARK to save space.

Stealth addresses and social recovery and multiple L2 wallets

For a long time, I have been interested in social recovery wallets, which have a multi-signature mechanism where keys can be shared among institutions, your other devices, and a combination of friends. If you lose your main key, the majority of keys allow for account access recovery.

However, social recovery wallets do not integrate well with stealth addresses: if you have to recover your account (changing the private key controlling it), you also have to perform some steps to change the account validation logic of your N stealth wallets, which would require N transactions at the cost of high fees, convenience, and privacy.

There are similar concerns regarding the interaction between social recovery and multiple L2 protocols: if you have accounts on Optimism, Arbitrum, StarkNet, Scroll, and Polygon, with a dozen parallel instances for scalability reasons, and you have an account on each instance, then changing keys can be a very complex operation.

Changing keys across multiple accounts on multiple chains is a huge task.

Perhaps you could use some automation software to transfer assets to new stealth addresses at random intervals over a two-week span to reduce the effectiveness of time-based associations. But this is far from perfect. Another approach is to secretly share the root key among guardians instead of using a smart contract for recovery. However, this would eliminate the ability to disable the guardians' power to help recover your account, posing long-term risks.

A more complex method involves zero-knowledge proofs. This allows for many accounts, even across many L2 protocols, to be controlled by a single k value somewhere (on the base chain or some L2), where changing that value is sufficient to change the ownership of all accounts, all without leaking your connections between multiple accounts.

Conclusion

The current basic stealth addresses can be quickly implemented and can significantly enhance user privacy on Ethereum. I believe that for other privacy-related reasons, wallets should start transitioning to a more native multi-address model (for example, creating a new address for each application you interact with might be an option).

However, stealth addresses do bring some long-term usability issues, such as the difficulty of social recovery. In the long run, these issues can be resolved, but the stealth address ecosystem does seem to heavily rely on zero-knowledge proofs.