3.1 Secret Engine

Recognizing that every zero-knowledge proof system consists of two parts: one is the algorithm, and the other is the polynomial commitment scheme. The initial phase of transforming a program into a zero-knowledge proof (ZKP) involves the algorithm. This process clarifies the relationship between these polynomials by establishing specific conditions among them.

Our zero-knowledge proof system is implemented based on the standard PlonK recipe, featuring highly customized gates, mainly including:

• Gadgets: Various gadgets used in game circuit development, including basic arithmetic circuits, hashing, ECC, zkshuffle, zkmatchmaking, etc. We recommend visiting our GitHub repository for more information about these gadgets.

• On-chain Verifier: Optimized PLONK/ZKVM for provers and verifiers, while supporting a universal reliable verifier for all EVM chains.

• Application-Specific Plonk: Using application-specific Plonk as the basic scheme for ZK proofs, with various gadgets provided by our SDK to write specific game circuits. We also provide verification contracts on different virtual machines (EVM/WASM/…) that can run on different blockchain systems, enabling off-chain proofs and on-chain verification.

Next, we will introduce two important components incubated by the Secret Engine: zkshuffle and zkmatchmaking.

3.1.1 ZK shuffle SDK

3.1.1.1 Introduction

Poker is a popular card game. In real life, the parties involved in the game can supervise each other to ensure fairness. With the rapid development of computer networks, players connected through the internet also have the opportunity to participate in poker games. However, ensuring the smooth conduct and fairness of the game in an online environment poses significant challenges, which is the problem that mental poker protocols aim to solve.

Mental poker is a card game constructed based on cryptographic principles. Since the first mental poker protocol was proposed by Shamir, Rivest, and Adleman in 1979【15】, research on the feasibility of mental poker games has begun. Mental poker is similar to regular poker gameplay, with the main difference being that mental poker is conducted in a network environment without physical cards, and all players are assumed to be dishonest, meaning cheating is possible. The first mental poker protocol is a two-party poker protocol that has been proven to have security vulnerabilities. According to literature【16】, a fair mental poker must satisfy the following properties:

1. Uniqueness: In traditional poker games, explicit card disclosure verifies that there are no duplicate cards. The mental poker protocol should guarantee the same property.

2. Random Distribution: In traditional poker games, one player shuffles the cards while others can observe in real-time, meaning the shuffling player cannot control the final shuffle result.

3. Confidentiality: At any time, if the deck is face down, no information about any card in the deck should be revealed. Additionally, when a player draws a card, other players should not be able to obtain any information about that card.

4. No Trusted Third Party: Relying on a trusted third party is not feasible, as anyone can be bribed, and there is no absolutely trustworthy third party.

In 1987, Crépeau proposed the first secure mental poker protocol【17】. Since then, mental poker protocol schemes have begun to emerge, but much of the research on mental poker protocols is based on TTP, as the academic community widely believes that using TTP is an effective way to ensure the fairness of mental poker protocols. However, poker, as a recreational game, often does not have a third party, and it is challenging to ensure the trustworthiness of a third party, especially in cases involving blockchain technology, where a trusted third party usually does not exist. Therefore, achieving a fair mental poker protocol without TTP is of great significance. The Barnett-Smart protocol【18】 proposed in 2003 provides two solutions based on the ElGamal and Pailler encryption systems, but the Pailler encryption scheme has a security limit, assuming that the number of colluding parties does not exceed (N-1)/2. Subsequently, the Castellà-Roca protocol【19】 was proposed, which adopted a different encryption scheme, and the shuffle process is faster than the Barnett-Smart protocol.

The overhead of the mental poker protocol mainly focuses on the shuffle part, but today, zero-knowledge proof algorithms have developed rapidly. For instance, geometry【20】【21】 points out that the shuffle process is no longer a bottleneck, and geometry believes that the Barnett-Smart protocol should divide the complete card game protocol into multiple secure sub-protocols: generating cards, masking, re-masking, shuffling, etc. These steps can be easily implemented as plug-and-play, and their security assumptions are based on Decisional Diffie-Hellman. Therefore, our mental poker protocol mainly draws on the Barnett-Smart protocol, but also considers that performing zkShuffle on a set of playing cards involves a large number of elliptic curve operations, resulting in a significantly large circuit size. To address this issue, we redesigned a zkshuffle-friendly TurboPlonk【22】 algorithm that significantly reduces the circuit gate size.

3.1.1.2 Basic Concepts

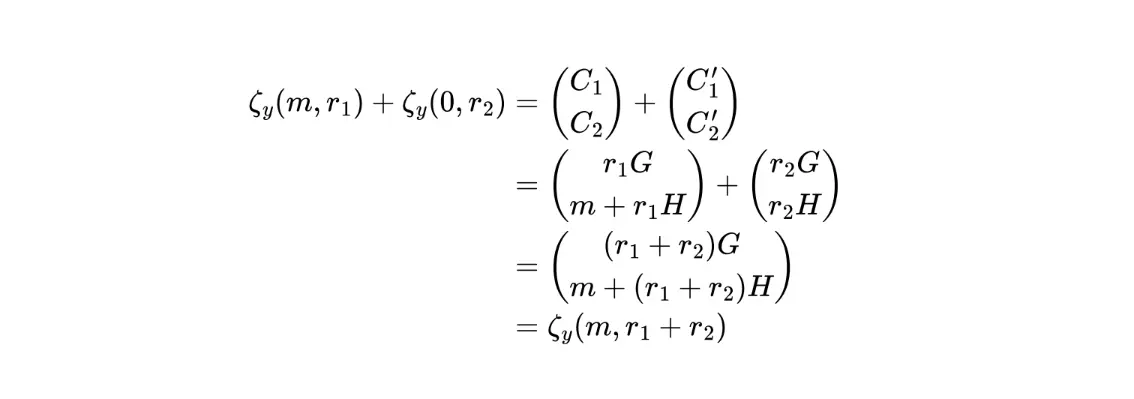
Note: n-out-of-n threshold EIGamal encryption【23】

3.1.1.3 Mental Poker Protocol

The mental poker protocol is not a single protocol but includes a set of sub-protocols, each responsible for a specific action.

• Key Generation:

• Generate public-private key pairs for each player.
• Aggregate all players' public keys to generate a single public key.

• Masking:

• The masking function is an ElGamal encryption function under the aggregated public key.

• Shuffle and Re-masking:

• Perform shuffling operations to randomize the cards.
• Mask the shuffled cards again.

• Unmask:

• Decode the cards to obtain the actual card information.

Key Generation Protocol

Masking Protocol

Re-Masking Protocol

Shuffle Argument

Unmask Protocol

3.1.1.4 Shuffle-Friendly PLONK Algorithm

The shuffle protocol mainly consists of two parts: 1) Permuting the cards; 2) Re-masking the cards; where the re-masking operation involves elliptic curve operations, specifically including 1 Constant-base scalar multiplication, 1 Non-constant-base scalar multiplication, and 2 curve additions. If using non-optimized TurboPlonk customized gates to write the arithmetic circuit, the number of circuit gates for re-masking a single card would be 596 + 1622 + 2 = 2220. Therefore, for a complete deck of cards (52 cards), the number of circuit gates would reach 115440, not including the gates related to permutation. Thus, if using non-optimized TurboPlonk to write the arithmetic circuit, the shuffle time would be very lengthy. To solve this problem, we re-engineered TurboPlonk to be friendly to shuffle operations, and it has been verified that only 85 gates are needed for a re-masking operation.

Note: Bowe Hopwood【24】

3.1.1.5 On-Chain Verification

Additionally, in our practice, we also encountered the issue of high gas fees for on-chain verification, and here we will mainly share our optimization insights.

Verifying the reveal of a card requires other players to provide the corresponding reveal information, along with a proof to verify the correctness of the reveal. The existing Geometry reality【25】 constructs a reveal proof based on the Chaum-Pedersen protocol, and we know that Chaum-Pedersen requires point multiplication operations, which are very expensive, mainly because Ethereum currently does not support the precompiled contract for the Baby Jubjub curve. According to test results, under the implementation based on Geometry, the gas cost for verifying the reveal proof reaches 7629888, which is clearly unacceptable.

Considering that Baby Jubjub is an embedded curve of BN254, we can use Snark for the reveal proof. According to gas analysis【26】, the on-chain verification cost for using Groth16 for the reveal proof is only about 200k, which is nearly 30 times lower than the native verification method. Compared to the native verification method, this seems like a very good choice. The reveal circuit is as follows:

In the future, we will perform proof aggregation to save gas to a greater extent.

Verifying shuffle in Texas Hold'em, we need to store the shuffled results on-chain, not only as the current shuffle result but also for subsequent shuffle circuit's public input. However, a deck of cards has 52 cards, totaling 208 uint256 type data, which incurs high on-chain storage costs.

Our solution is to only store part of the card data on-chain. Specifically, we only need to store 2n + 5 cards, where n is the number of players. Considering that our game supports a maximum of 6 players simultaneously, we will use at most 17 cards. This means we ultimately only need to store 17 cards on-chain, saving 2/3 of the storage costs.

Although we ultimately only need to store 17 cards on-chain, another purpose of on-chain storage mentioned earlier is that these cards will also serve as public input for the subsequent shuffle circuit. Therefore, if we only store 17 cards, we cannot verify the correctness of the shuffle. To solve this problem, our Shuffle circuit will additionally output a hash of the complete deck of cards, which will be stored on-chain. When verifying zkShuffle, it will serve as the public input of the circuit, thereby ensuring the correctness of the shuffle.

3.1.2 ZK matchmaking SDK

Matchmaking is a mechanism designed to ensure that players can compete against opponents of similar skill levels, thereby providing a fair and enjoyable gaming experience. The core objectives of matchmaking can be summarized as follows:

• Fair Competition: Provide players of comparable skill levels to compete against each other, so that both sides have a winning probability as close to 50% as possible.

• Unpredictability: The matchmaking process should be unpredictable, meaning the final competitors should be unpredictable.

Overall Process

1. When applying to become a Prover, a seed must be committed to the contract, which only the Prover knows.

2. Players send a request to join the game.

3. After the sorter receives the request, it sorts based on the ranking strategy and then sends the generated queue to both the contract and the prover.

4. The Prover performs random matching on different queues based on zkSnark, with the matching results depending on the seed committed by the Prover, the input queue, and the on-chain random number (which is determined but unpredictable), and then sends the matching results and proof to the contract.

5. The contract performs on-chain verification, and if verification passes, players enter the game based on the matching results.

On the blockchain, we can easily obtain on-chain random numbers like block hashes, but they are susceptible to block withholding attacks from miners and validators, making on-chain random numbers like block hashes not very secure, thus challenging the unpredictability of matchmaking. Verifiable Random Functions (VRF) are a type of random number generator with verification properties that can generate statistically uniform and unpredictable random outputs, and their outputs are verifiable, providing a good solution for our on-chain random numbers. Let’s briefly understand the principle of VRF, which takes a seed as input and outputs a random number.

In addition to on-chain random numbers, unpredictability also relies on the seed committed by the Prover, and we will construct a penalty mechanism to prevent the Prover from arbitrarily leaking random numbers.

References:

【15】A. Shamir, R. L. Rivest and L. M. Adleman, Mental poker, Technical report LCS/TM-125, Massachusetts Institute of Technology, April 1979.
【16】Crépeau C. A secure poker protocol that minimizes the effect of player coalitions, in: Conference on the Theory and Application of Cryptographic Techniques. Berlin, Heidelberg: Springer Berlin Heidelberg, 1985: 73--86.
【17】C. Crepeau, A zero-knowledge poker protocol that achieves confidentiality of the players' strategy or how to achieve an electronic poker face, in: Advances in Cryptology -- Crypto 086, Lecture Notes in Computer Science 263, Springer-Verlag, Berlin (1987), 239--247.
【18】A. Barnett and N. Smart, Mental poker revisited, in: Cryptography and Coding, Lecture Notes in Computational Science 2898, Springer-Verlag, Berlin (2003), 370--383.
【19】J. Castellà-Roca, Contributions to mental poker, Ph.D. Thesis, Autonomous University of Barcelona, Doctoral Programme in Computer Science and Artificial Intelligence, 2005.
【20】N Mohnblatt, A Novakovic and K Gurkan, Mental Poker in the Age of SNARKs - Part 1,
https://geometry.xyz/notebook/mental-poker-in-the-age-of-snarks-part-1
【21】N Mohnblatt, A Novakovic and K Gurkan, Mental Poker in the Age of SNARKs - Part 1,
https://geometry.xyz/notebook/mental-poker-in-the-age-of-snarks-part-2
【22】Gabizon A, Williamson Z J. The turbo-plonk program syntax for specifying snark programs, in: ZKProof Workshop. 2020, 3.
【23】Desmedt Y. Threshold cryptosystems, in: International Workshop on the Theory and Application of Cryptographic Techniques. Berlin, Heidelberg: Springer Berlin Heidelberg, 1992: 1--14.
【24】https://github.com/arkworks-rs/crypto-primitives/tree/main/crypto-primitives/src/crh/bowe_hopwood.

【25】https://github.com/geometryxyz/mental-poker/blob/main/barnett-smart-card-protocol/src/discretelogcards/mod.rs#L320.

【26】Todd Norton, Groth16 Verification Gas cost,https://hackmd.io/@nebra-one/ByoMB8Zf