一文で理解するFOAKSにおける多項式コミットメント協定のブレイクダウン
執筆:Fox Tech CEO 康水跃、Fox Tech チーフサイエンティスト 孟铉济
前言:もし暗号学者がテンソル積(Tensor Product)と多項式の値の関係を発見しなかったならば、多項式コミットメントプロトコルBrakedownは難しく、Brakedownに基づくOrionやFOAKSのような全く新しい高速アルゴリズムも誕生しなかったでしょう。
多くの多項式コミットメントに依存するゼロ知識証明システムの中で、異なるコミットメントプロトコルが使用されています。a16zのJustin Thalerが2022年8月に発表した記事「Measuring SNARK performance: Frontends, backends, and the future」によると、BrakedownはProof Sizeが大きいにもかかわらず、現在最も速い多項式コミットメントプロトコルであることは間違いありません。
FRI、KZG、Bulletproofはより一般的な多項式コミットメントプロトコルですが、速度がボトルネックとなっています。zkSyncが採用しているPlonky、Polygon zkEVMが採用しているPlonky2、Scrollが採用しているUltra-Plonkなどのアルゴリズムは、KZGに基づく多項式コミットメントです。Proverは多くのFFT計算とMSM演算を含み、多項式とコミットメントを生成しますが、これらは計算負担を大きくもたらします。MSMはマルチスレッド加速の可能性がありますが、大量のメモリを必要とし、高い並列性でも遅く、大規模なFFTはアルゴリズムの実行時データの頻繁なシャッフルに大きく依存しており、分散加速を通じて計算クラスターを跨いでのロードが困難です。
より高速な多項式コミットメントプロトコルBrakedownのおかげで、これらの計算の複雑さが大幅に低下しました。
FOAKS、すなわちFast Objective Argument of Knowledgesは、Fox Techが提案したBrakedownに基づくゼロ知識証明システムフレームワークです。FOAKSはOrionを基にしてFFT計算をさらに削減し、最終的にはFFTを排除することを目指しています。さらに、FOAKSは証明サイズを削減するための非常に巧妙な新しい証明再帰方式を設計しました。FOAKSフレームワークの利点は、線形証明時間を実現しながら、証明サイズが小さいことで、zkRollupシナリオに非常に適しています。
以下では、FOAKSが使用する多項式コミットメントプロトコルBrakedownについて詳しく説明します。
暗号学において、コミットメント(Commitment)プロトコルは、証明者(Prover)が特定の秘密値に対してコミットし、公開のコミットメント値を生成します。このコミットメント値はバインディング(Binding)とハイディング(Hiding)の特性を持ち、その後、提出者はこのコミットメントを開き、メッセージを検証者に送信して、コミットメントとメッセージの対応関係を検証します。この点で、コミットメントプロトコルとハッシュ関数の役割には多くの共通点がありますが、コミットメントプロトコルは公的鍵暗号学の数学的構造に依存することが多いです。一方、多項式コミットメント(Polynomial Commitment)は多項式に対するコミットメントスキームの一種であり、つまりコミットされた値が多項式であることを意味します。また、多項式コミットメントプロトコルには、指定された点での値を取得し、証明を提供するアルゴリズムも含まれており、これにより多項式コミットメントプロトコル自体が重要な暗号学プロトコルの一種となり、多くのゼロ知識証明システムの核心部分となっています。
最新の暗号学の研究において、テンソル積(Tensor Product)と多項式の値の関係が発見されたため、これに関連する一連の多項式コミットメントプロトコルが誕生しました。Brakedownはその代表的なプロトコルです。
Brakedownのプロトコルの詳細を説明する前に、いくつかの基礎知識を理解する必要があります。まず、線形符号(Linear Code)、衝突耐性ハッシュ関数(Hash Function)、マークルツリー(Merkle Tree)、テンソル積(Tensor Product)の演算、および多項式の値のテンソル積表現について理解する必要があります。
まず、線形符号(Linear Code)についてです。メッセージの長さがk、符号語の長さがnの線形符号は、メッセージから符号語への単射が存在する線形部分空間CFnであり、これをエンコーディングと呼び、記号EC:FkCで表します。任意の符号語の線形結合は依然として符号語です。二つの符号語u、vの距離は彼らのハミング距離であり、記号(u,v)で表します。最短距離はd=minu,v(u,v)です。このような符号は[n,k,d]線形符号と記述され、dnで符号の相対距離を表します。
次に、衝突耐性ハッシュ関数(Hash Function)とマークルツリー(Merkle Tree)についてです。
H:{0,1}2{0,1}をハッシュ関数として表します。マークルツリーは特別なデータ構造であり、2d個のメッセージに対するコミットメントを実現し、ハッシュ値hを生成します。任意のメッセージを開く際にはd+1個のハッシュ値が必要です。
マークルツリーは深さdの二分木として表現でき、L個のメッセージ要素m1,m2,…,mlはそれぞれ木の葉に対応します。木の各内部ノードはその二つの子ノードによってハッシュ計算されます。メッセージmiを開く際には、miから根ノードへのパスを公開する必要があります。
以下の記号で表します:
hMerkle.Commit(m1,…,ml)
(mi,i)Merkle.Open(m,i)
{0,1}Merkle.Verify(i,mi,h)
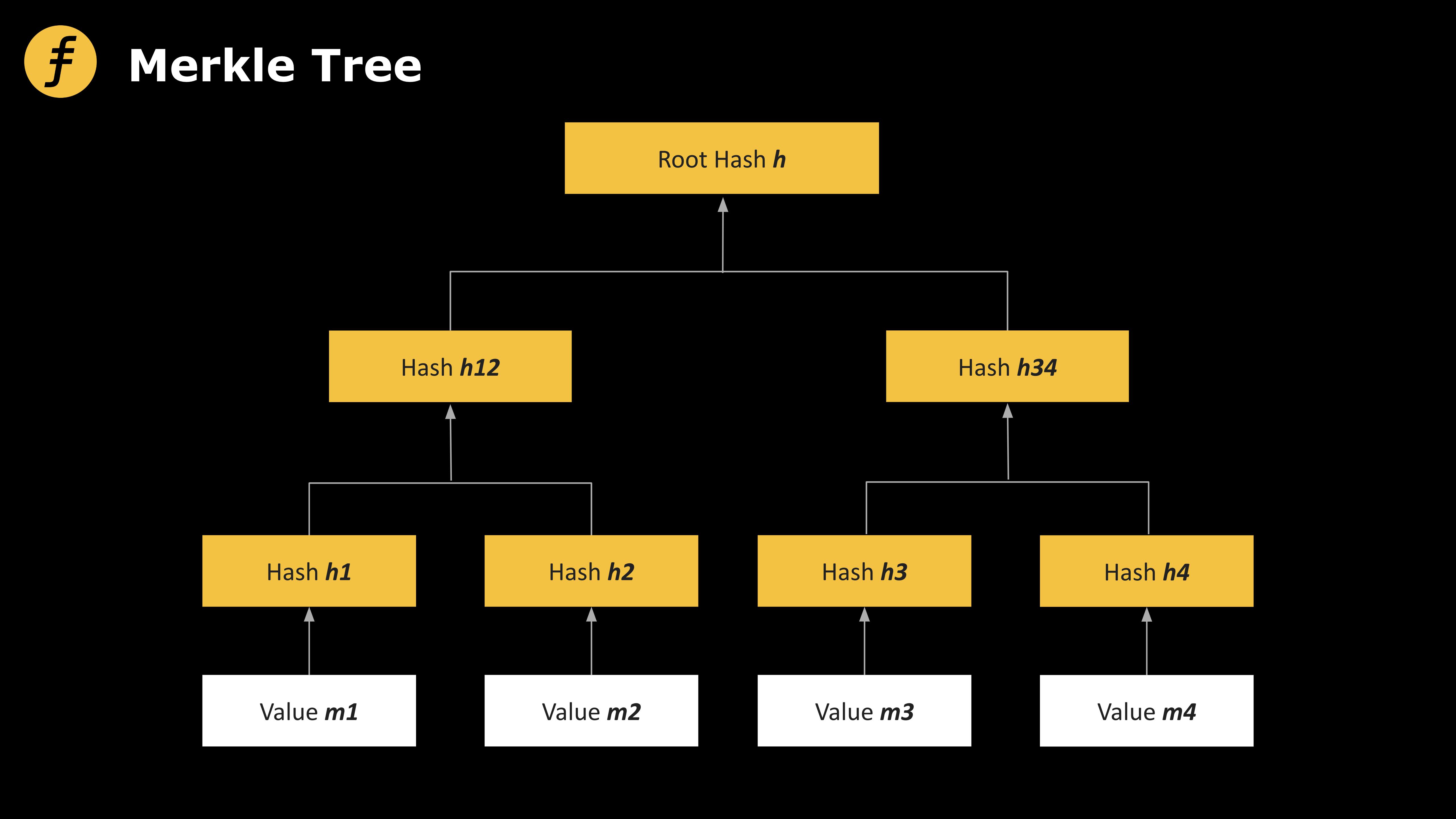
図1:マークルツリー(Merkle Tree)
次に、テンソル積(Tensor Product)の演算がどのように行われるかを理解する必要があります。数学的に、テンソルはベクトルと行列を高次元空間に拡張したものであり、重要な研究対象です。テンソルについての詳細な議論は本稿の範囲を超えていますが、ここではベクトルと行列のテンソル積演算について紹介します。
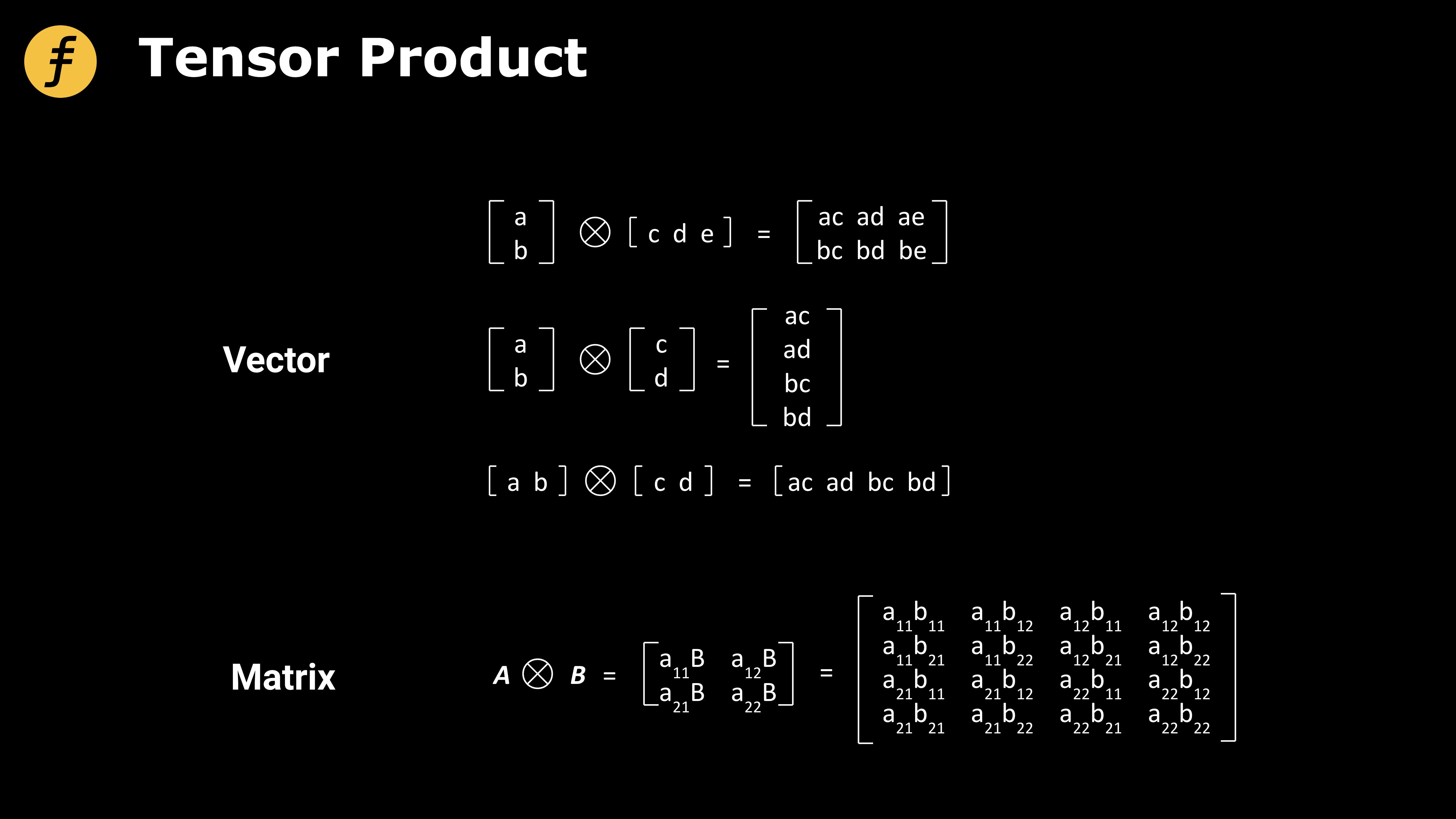
図2:ベクトルと行列のテンソル積演算
続いて、多項式の値のテンソル積表現について知る必要があります。
[GLS+]では、多項式の値はテンソル積の形式で表現できることが述べられています。ここでは多変数多項式のコミットメントを考えます。
具体的には、与えられた多項式がベクトルx0,x1,…,xlogN-1の値を次のように表すことができます:
(x0,x1,…,xlogN-1)=i0=01i1=01…ilogN-1=01wi0i1…ilogN-1x0i0x1i1…xlogN-1ilogN-1
多変数の定義に従い、各変数の次数は0または1であるため、ここにはN個の単項式と係数、そしてlogN個の変数があります。i=j=0logN-12jijとし、i0i1…ilogN-1はiの二進数表現です。wを多項式係数とし、w[i]=wi0i1…ilogN-1と定義します。同様に、Xi=x0i0x1i1…xlogN-1ilogN-1と定義します。k=N,r0={X0,X1,…,Xk-1},r1={X0k,X1k,…,Xk-1k}とします。したがって、X=r0r1となります。
したがって、多項式の値はテンソル積の形式で表現できます:(x0,x1,…,xlogN-1)=\<w,r0r1>。
最後に、FOAKS、Orion[XZS22]で使用されるBrakedownのプロセスを見てみましょう。
まず、PC.Commitは多項式係数wをkkの行列形式に分割し、エンコードします(「予備知識」の線形符号を参照)。これをC2と記します。その後、C2の各列C2[:,i]に対してコミットメントを行い、マークルツリーを構築します。そして、各列から形成されたマークルツリーの根を用いて、最終的なコミットメントとして別のマークルツリーを構築します。
値の証明計算においては、二つの点を証明する必要があります。一つは近接性(Proximity)、もう一つは一貫性(Consistency)です。近接性は、コミットされた行列が実際にエンコードされた符号語に十分近いことを保証します。一貫性はy=\<w,r0r1>を保証します。
近接性検証:近接性検証は二つのステップから成ります。まず、検証者は証明者にランダムベクトル0を送信し、証明者は0とC1の内積を計算します。これは0の成分を係数としてC1の行の線形結合を計算することを意味します。線形符号の性質により、C0はy0の符号語です。その後、証明者はC0が実際にコミットされた符号語から計算されたことを証明します。これを証明するために、検証者はt列をランダムに選択し、証明者は対応する列を開示し、マークルツリーの証明を提供します。検証者はこれらの列と0の内積がC0の対応する位置と等しいかを確認します。[BCG20]では、使用される線形符号が定数の相対距離を持つ場合、コミットされた行列は圧倒的な確率で符号語に近いことが証明されています(圧倒的な確率とは、命題の否定が成立する確率が無視できることを指します)。
一貫性検証:一貫性検証は近接性検証のプロセスと完全に類似しています。異なる点は、ランダムベクトル0を使用するのではなく、直接r0を使用して線形結合の部分を完成させることです。同様に、c1もメッセージy1の線形符号であり、(x)=\<y1,r1>です。[BCG20]では、一貫性検証を通じて、コミットされた行列が符号語に近い場合、圧倒的な確率でy=(x)が成立することが証明されています。
擬似コード形式で、Brakedownプロトコルのプロセスを示します:
Public input :評価点X、テンソル積X=r0r1として解析される;
Private input :多項式、係数はwで表される。
Cを[n,k,d]-線形符号とし、EC:FkFnをエンコーディング関数とし、N=kkとします。Nが完全平方数でない場合、次の完全平方数にパディングできます。Pythonスタイルの表記mat[:,i]を使用して、行列matのi番目の列を選択します。
function PC. Commit():
wをkkの行列として解析します。証明者はローカルでテンソルコードエンコーディングC1、C2を計算します。C1はkn行列、C2はnn行列です。
for i [n] do
マークルツリーの根Roott=Merkle.Commit(C2[:,i])を計算します。
マークルツリーの根R=Merkle.Commit([Root0,……Rootn-1])を計算し、Rをコミットメントとして出力します。
function PC. Prover(, X, R)
証明者は検証者からランダムベクトル0Fkを受け取ります。
近接性:C0=i=0k-10[i]C1[:,i],y0=i=0k-10[i]w[i]
一貫性:C1=i=0k-1r0[i]C1[:,i],y1=i=0k-1r0[i]w[i]
証明者はC1,y1,C0,y0を検証者に送信します。
検証者はt[n]を配列Iとしてランダムにサンプリングし、証明者に送信します。
for idxI do
証明者はC1 [:,idx]とRの下でC2 [:,idx]のマークルツリー証明を検証者に送信します。
function PC. VERIFY_EVAL(X,X,y=(X),R)
近接性:idxI,C0[idx]==\<0,C1[:,idx]>およびEC(y0)==C0
一貫性:idxI,C1[idx]==\<r0,C1[:,idx]>およびEC(y1)==C1
y==\<r1, y1>
idxI, EC(C1[:,idx])はROOTidxと一貫しており、ROOTidxのマークルツリー証明は有効です。
すべての条件が満たされていればacceptを出力します。そうでなければrejectを出力します。
結語:多項式コミットメントは非常に重要な暗号学プロトコルであり、多くの暗号システム、特にゼロ知識証明システムで広く使用されています。本稿では、多項式コミットメントBrakedownプロトコルとそれに関連する数学的知識について詳しく説明しました。FOAKSの重要な基盤コンポーネントとして、BrakedownはFOAKSのインスタンス化性能の向上に重要な役割を果たしています。
参考文献
[GLS+]:Alexander Golovnev, Jonathan Lee, Srinath Setty, Justin Thaler, and Riad S. Wahby. Brakedown: Linear-time and post-quantum snarks for r1cs. Cryptology ePrint Archive. https://ia.cr/2021/1043.
[XZS22]:Xie T, Zhang Y, Song D. Orion: Zero knowledge proof with linear prover time[C]//Advances in Cryptology--CRYPTO 2022: 42nd Annual International Cryptology Conference, CRYPTO 2022, Santa Barbara, CA, USA, August 15--18, 2022, Proceedings, Part IV. Cham: Springer Nature Switzerland, 2022: 299-328.https://eprint.iacr.org/2022/1010
[BCG20]:Bootle, Jonathan, Alessandro Chiesa, and Jens Groth. "Linear-time arguments with sublinear verification from tensor codes." Theory of Cryptography: 18th International Conference, TCC 2020, Durham, NC, USA, November 16--19, 2020, Proceedings, Part II 18 . Springer International Publishing, 2020.
Justin Thaler from A16zcrypto, Measuring SNARK performance: Frontends, backends, and the future
https://a16zcrypto.com/measuring-snark-performance-frontends-backends-and-the-future/テンソル積の紹介:https://blog.csdn.net/chenxy_bwave/article/details/127288938