ゼロ知識証明の力：zk-SNARKを深く理解する

编译：DODO Research

作者：0xAlpha Co-founder @DeriProtocol

イントロダクション

zk-SNARK、すなわち「ゼロ知識簡潔非対話的証明」は、検証者が証明者が特定の知識（ウィットネスと呼ばれる）を持っていることを確認できるようにし、特定の関係を満たすものであり、ウィットネス自体に関する情報を明らかにすることなく行われます。

• 特定の問題に対してzk-SNARKを生成するには、以下の4つの段階があります：
• 問題（または関数）を算術ゲート回路に変換します。
• 次に、この回路を行列式に翻訳します。
• この行列式はさらに多項式に変換され、この多項式は特定の最小多項式で割り切れる必要があります。

最後に、この割り切れ性は有限体の楕円曲線点で表現され、証明が行われます。

最初の3つのステップは、元の表現の変換に過ぎません。最後のステップでは、同型暗号を使用して3番目のステートメントを暗号空間に投影し、証明者がその中のミラー表現を確認できるようにします。この投影は非対称暗号を利用しているため、3番目のステートメントから元のステートメントに遡ることは不可能であり、ゼロ知識の露出を確保します。

この記事を読むために必要な数学的背景は、STEM専攻の学生の1年生の代数レベルに相当します。唯一挑戦的な概念は、楕円曲線暗号かもしれません。これに不慣れな人は、特別な基数を持つ指数関数として考えることができ、逆関数はまだ解決されていないことを覚えておいてください。

この記事では、以下の記号規則に従います：

行列：太字の大文字、例えばA；明示的な形式は
ベクトル：矢印付きの小文字、明示的な形式は[ ]；デフォルトではすべてのベクトルは列ベクトル
スカラー：通常の文字で表現

この問題を例として考えてみましょう：

f(x)=x\^3+x\^2+5 (1)

アリスが彼女が知っていることを証明したいと仮定します。私たちは、アリスが彼女の証明のためにzk-SNARKを生成するために必要な全プロセスを段階的に紹介します。
この問題は、制御フロー（例えば、if-then-else）を含まないため、あまりにも単純に見えるかもしれません。しかし、制御フローを持つ関数を算術表現に変換することは難しくありません。例えば、次の問題（またはプログラミング言語での「関数」）を考えてみましょう：

f(x, z):
if(z==1):
return x*x*x+x*x+5
else:
return x*x+5

この問題を次の算術式に書き換えるのは簡単です（zが(0,1)に属すると仮定すると）、これは方程式(1)とそれほど複雑ではありません。

f(x,z)=(z-1)(x\^2+5)+z(x\^3+x\^2+5)

この記事では、議論の基礎として方程式(1)を引き続き使用します。

第1ステップ：算術ゲート回路

方程式(1)は以下の基本的な算術演算に分解できます：

これは以下の算術ゲート回路に対応します：

私たちはまた、方程式(2)を4つの「一次制約」のセットと呼びます。各制約は回路内の1つの算術ゲートの関係を説明します。通常、n個の一次制約のセットは二次算術プログラム（QAP）として要約できます。次に説明します。

第2ステップ：行列

まず、「ウィットネス」ベクトルを次のように定義しましょう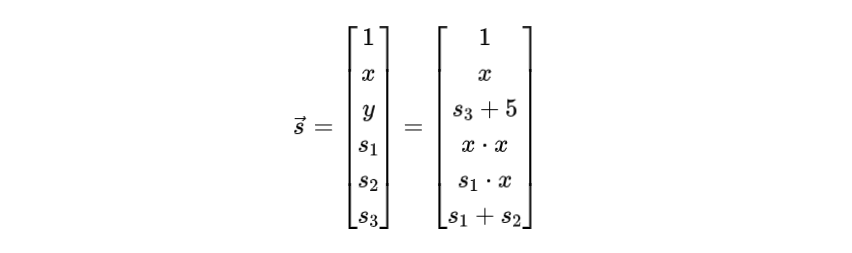：ここでy, s1,s2,s3は方程式(2)で定義されたものと同じです。
通常、m個の入力とn個の算術ゲートを持つ問題（すなわちn-1個の中間ステップと最終出力）に対して、このウィットネスベクトルは(m+n+1)次元になります。実際の問題では、数字nは非常に大きくなる可能性があります。例えば、ハッシュ関数の場合、nは通常数千です。

次に、3つのn*(m+n+*1)行列A,B,Cを構築し、方程式(2)を次のように書き換えます：

方程式(3)は方程式(2)の別の表現に過ぎません：各(ai,bi,ci)のセットは回路内の1つのゲートに対応します。私たちは明示的に行列式を展開するだけでこれを確認できます：

したがって、LHS=RHSは方程式(2)と完全に同じであり、行列方程式の各行は1つの一次制約（すなわち回路内の1つの算術ゲート）に対応します。

私たちは(A,B,C)の構築ステップを省略しましたが、実際にはこれらのステップは比較的簡単で直接的です。私たちは対応する一次制約に基づいてそれらを行列形式に変換し、(A,B,C)の各行の内容、すなわち(ai,bi,ci）を決定するだけです。最初の行の例を挙げると、最初の一次制約xとxを掛け合わせてs1になるためには、[0,1,0,0,0]、[0,1,0,0,0]、および[0,0,0,1,0,0]をベクトルsと掛け合わせる必要があります。

したがって、私たちは算術ゲート回路を行列式に変換することに成功しました。すなわち方程式(3)です。同時に、証明する必要があるオブジェクトは、ウィットネスベクトルsに変わりました。

第3ステップ：多項式

今、私たちはzに関する多項式のセットを定義するn*(*n+m+*1)行列PAを構築します：

これらは6つの変数の4組の線形方程式であり、従来の方法で解決できます。しかし、この場合、PAを解決するより効率的な方法はラグランジュ補間であり、問題の特異性を利用します。ここでは、PAを解決するプロセスを省略しますが、少し煩雑ですが非常に直接的です。

ここで：

第4ステップ：楕円曲線点

方程式(4)を次のように書き換えます：

ここでi(z)=1はzの平凡な零次多項式であり、方程式を統一するために使用されます------すべての項は二次です。このようにする必要性はすぐに明らかになります。この方程式はzに関する多項式の加法と乗法のみを含んでいます。

次に、実際の操作手順について詳しく説明します。

楕円曲線暗号

楕円曲線の一般理論はこの記事の範囲を超えています。この記事の目的において、楕円曲線は素体FpからE関数にマッピングされ、Eはy\^2=x\^3+ax+bを満たす点（楕円曲線点、略してECP）を含みます。

ここで注意すべきは、これまで通常の算術について議論してきましたが、今や素体に変換すると、数字の算術演算はモジュロ演算の形で行われるということです。例えば、a+b=a+b(mod p)であり、ここでpはFpの階です。

一方、2つの楕円曲線点の加法は以下のように定義されます：

具体的には、2つのECPs PとQの加法：

直線PQと曲線Rの交点を見つけ、-(P+Q)として定義します。
曲線Rの「ミラー」点R'に反転します。
したがって、楕円曲線点の加法P+Q=R'と定義します：

このルールは、特別な場合、すなわちECPが自加する場合にも適用され、この場合はその点の接線を使用します。

今、私たちはランダムに点Gを選び、数字1をその上にマッピングします。（この「初期マッピング」は少し任意に聞こえるかもしれません。後で議論します）。次に、任意のnがFpに属する場合、私たちは次のように定義します：

E(N)=G+ G+ G+ …..+G=G点乗n

これは操作表現を持っています。+Gの操作を「生成器」と定義し、gと記します。したがって、上記の定義は次のように等価です：

楕円曲線に不慣れな人にとって、このマッピングは通常の指数関数に類似しており、基数gが実数に置き換わります。算術演算の挙動は似ています。しかし、重要な違いは、g\^nの逆関数を計算することが実行不可能であるということです。つまり、楕円曲線バージョンのを計算する方法はありません。これはもちろん、楕円曲線暗号の基礎です。このようなマッピングは単方向暗号と呼ばれます。

注意すべきは、与えられた楕円曲線に対して、Gを選択すること（したがって「生成器」gを選択すること）が任意であるため（x軸上の点を除いて）、無限のマッピング方法があるということです。（Gまたはgを選択すること）は、指数関数の基数（2\^x,10\^x,e\^xなど）を選択することに類似しており、常識の一部です。

しかし、アリスが証明したい方程式(5)は二次形式であるため、線形では不十分です。二次項を処理するために、暗号空間で乗法を定義する必要があります。これはペアリング関数、または双線形マッピングと呼ばれ、次に説明します。

双線形マッピング

公共参照文字列

全体のプロセスは「検証鍵」と呼ばれ、略してVKと呼ばれます。ここでは、7つの楕円曲線点（ECPs）だけが検証者に提供される必要があります。問題に関与する入力や一次制約の数に関係なく、VKは常に7つのECPsから構成されることに注意してください。

また、「信頼できる設定」と特定の問題に対してPKとVKを生成するプロセスは、一度操作するだけで済むことも言及する価値があります。

証明と検証

今、公鍵（PK）を持っているアリスは、次の楕円曲線点（ECPs）を計算します：

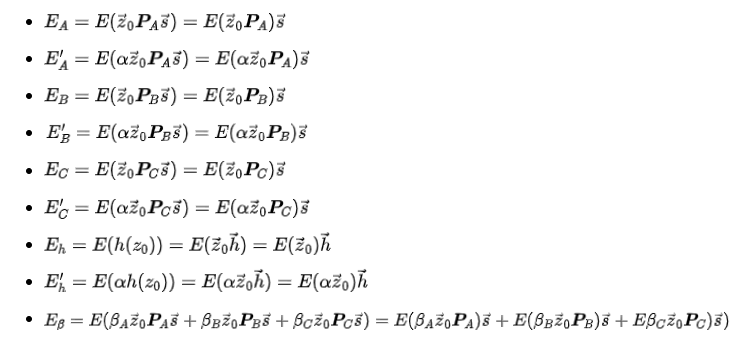
これらの9つの楕円曲線点がゼロ知識簡潔非対話的証明（zk-SNARK）の鍵です！

注意してください、アリスは実際には公鍵内の楕円曲線点に対して線形結合演算を行っただけです。この点は特に重要で、検証時に重点的にチェックされます。

今、アリスはzk-SNARK証明を提出し、私たちはついに検証段階に入ります。これは3つのステップで行われます。

まず、最初の8つの楕円曲線点が本当に一般的な参照文字列の点の線形結合であることを確認する必要があります。

この3つのチェックがすべて成立すれば、等式（5）が検証され、私たちはアリスがウィットネスを知っていると信じます。等式の背後にある理由を説明しましょう。最初の部分の最初の等式を例にとると、等式が成立するのは双線形性の性質によるものです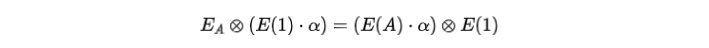：しかし、アリスはシンボルアルファの値を知らないため、この加法を明示的に計算することはできません。彼女が等式を満たす(EA,EA')のペアを考え出す唯一の方法は、同じベクトルsのセットを使用して、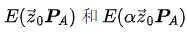の2つの組み合わせを計算することです。

参考文献

"Zk-SNARKs: Under the Hood" (Vitalik Buterin)

"A Review of Zero Knowledge Proofs" (Thomas Chen, Abby Lu, Jern Kunpittaya, and Alan Luo)

"Why and How zk-SNARK Works: Definitive Explanation" (Maksym Petkus)

Website: Zero-Knowledge Proofs

Wikipedia: Elliptic curve

Wikipedia: Finite field

Wikipedia: Pairing-based cryptography