Scroll 창립자 장예: zkEVM 설계, 최적화 및 응용

스크롤

2023-04-20 12:10:49

수집

Scroll은 zkRollup의 이더리움 범용 확장 솔루션을 구축하고 있으며, 매우 진보된 산술 회로와 증명 시스템을 사용하고, 하드웨어 가속을 통해 빠른 검증기와 증명 재귀를 구축하고 있습니다.

위챗으로 스캔하기

원문 저자：Ye Zhang

원문 출처：Scroll CN

편집：F.F

최신 ZKP Mooc 과정에서 Scroll의 공동 창립자 장예는 zkEVM 설계, 최적화 및 응용에 대한 발표를 했습니다. Scroll은 이더리움과 동등한 ZK-Rollup을 구축하고 있으며, 바이트코드 수준의 호환성을 제공하여 모든 기존 도구를 직접 지원합니다.

다음은 비디오의 청취 기록 텍스트 버전입니다.

발표는 네 부분으로 나뉘어 있으며, 첫 번째 부분에서 장예는 개발 배경과 우리가 왜 처음에 zkEVM이 필요한지, 그리고 왜 최근 2년 동안 그렇게 인기를 끌게 되었는지에 대해 소개했습니다. 두 번째 부분에서는 전체 프로세스를 통해 zkEVM을 처음부터 구축하는 방법을 설명하며, 여기에는 산술화 및 증명 시스템이 포함됩니다. 세 번째 부분에서는 Scroll이 zkEVM을 구축하는 과정에서 직면한 문제를 흥미로운 연구 문제를 통해 논의합니다. 마지막으로 zkEVM을 사용하는 다른 응용 프로그램에 대해 소개합니다.

배경 및 동기

전통적인 Layer 1 블록체인은 일부 노드가 P2P 네트워크를 통해 공동으로 유지 관리됩니다. 그들은 사용자 거래를 수신하면 EVM의 가상 머신 내에서 실행하고, 계약을 호출하고 저장하며, 거래에 따라 전역 상태 트리를 업데이트합니다.

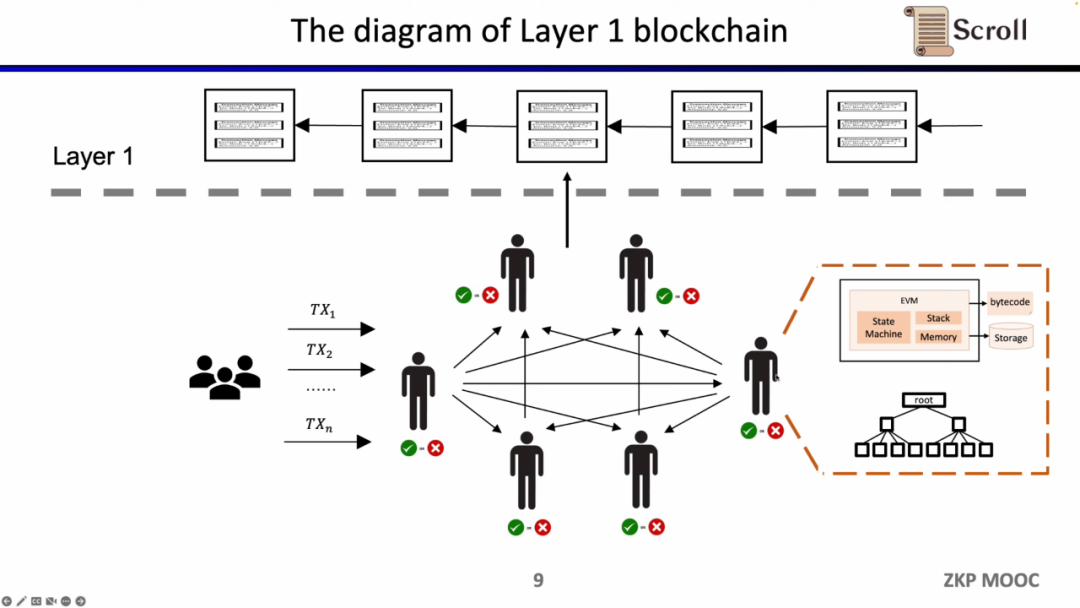
이러한 아키텍처의 장점은 탈중앙화와 보안성이지만, 단점은 L1에서의 거래 수수료가 비싸고 거래 확인이 느리다는 것입니다.

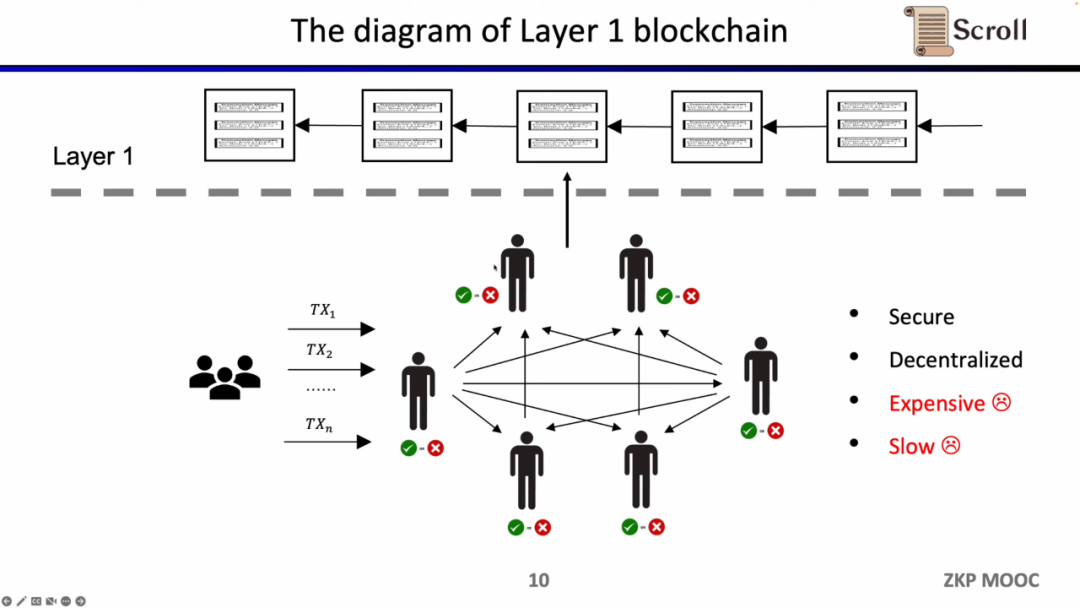
ZK-Rollup 아키텍처에서는 L2 네트워크가 데이터와 데이터의 유효성을 증명하는 증명만 L1에 업로드하면 됩니다. 이 증명은 제로 지식 증명 회로를 통해 계산됩니다.

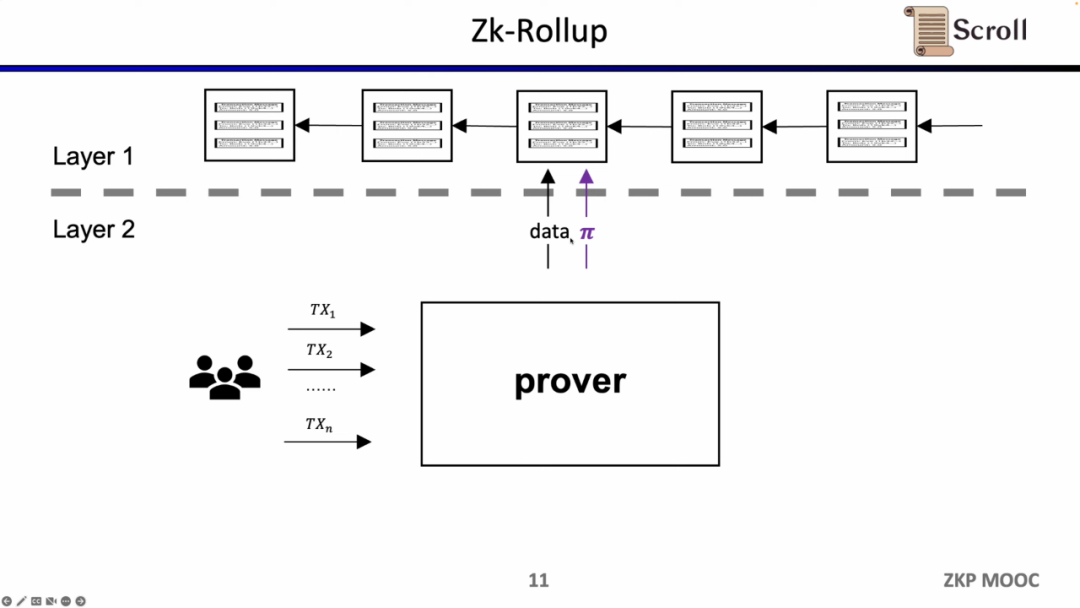
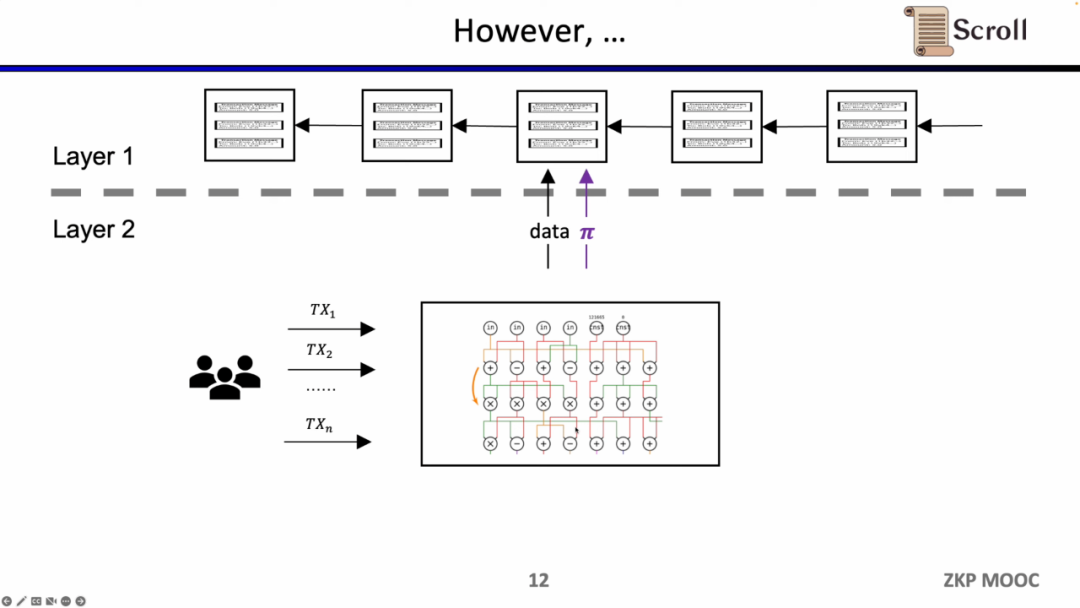
초기 ZK-Rollup에서는 회로가 특정 응용 프로그램에 맞게 설계되었으며, 사용자는 거래를 서로 다른 증명자에게 보내야 했습니다. 그런 다음 서로 다른 응용 프로그램의 ZK-Rollup은 자신의 데이터와 증명을 L1에 제출합니다. 이로 인해 원래 L1 계약의 조합 가능성이 상실되는 문제가 발생했습니다.

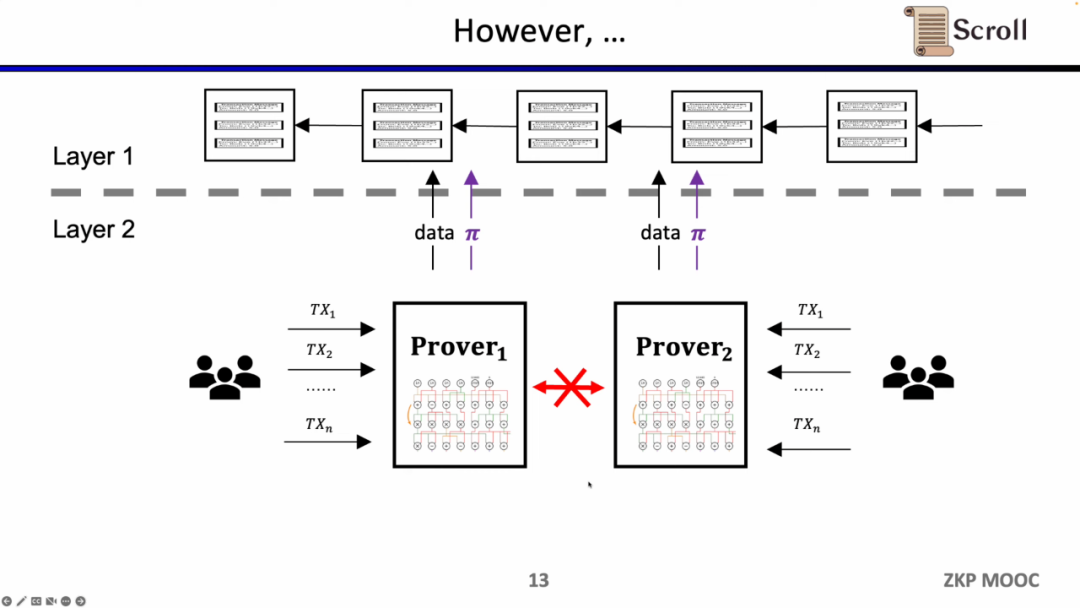
Scroll이 하려는 것은 본질적인 zkEVM 솔루션으로, 일반적인 ZK-Rollup입니다. 이는 사용자에게 더 친숙할 뿐만 아니라 개발자에게도 L1에서의 개발 경험을 제공합니다. 물론 그 뒤에는 매우 큰 개발 난이도가 있으며, 현재의 증명 생성 비용도 매우 높습니다.

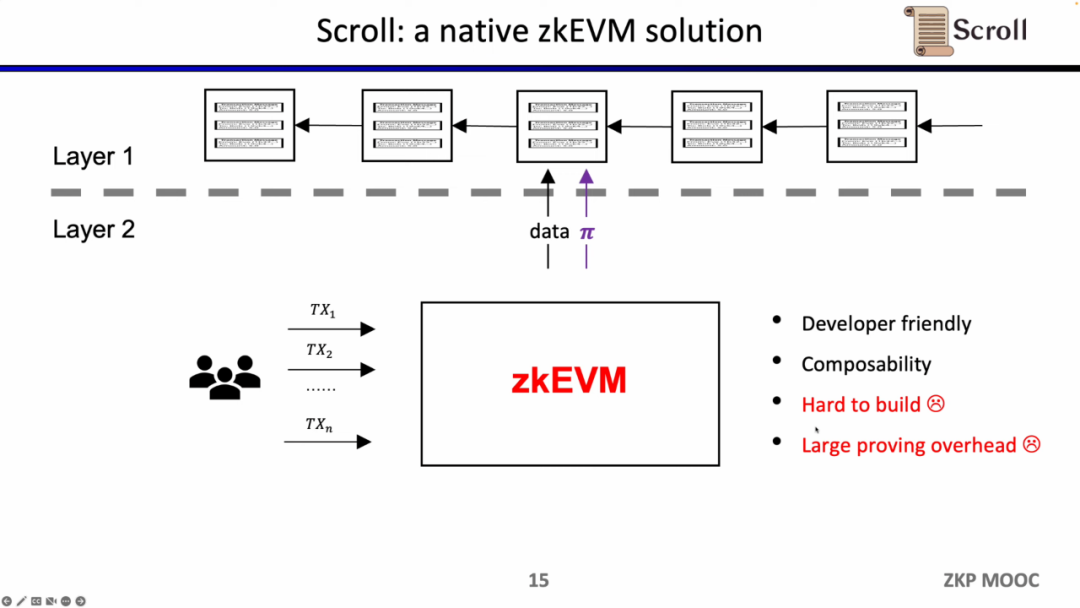
다행히도, 제로 지식 증명의 효율성이 지난 2년 동안 크게 향상되었습니다. 이것이 최근 2년 동안 zkEVM이 그렇게 인기를 끌게 된 이유입니다. 최소한 네 가지 이유가 그것을 가능하게 했습니다. 첫 번째는 다항식 약속의 출현으로, 이전 Groth16 증명 시스템에서는 제약의 규모가 매우 컸지만, 다항식 약속은 더 높은 차수의 제약을 지원하여 증명 규모를 줄일 수 있습니다. 두 번째는 조회 테이블과 사용자 정의 게이트의 출현으로, 더 유연한 설계를 지원하여 증명을 더욱 효율적으로 만들 수 있습니다. 세 번째는 하드웨어 가속의 돌파구로, GPU, FPGA 및 ASIC을 통해 증명 시간을 1-2 배 줄일 수 있습니다. 네 번째는 재귀 증명 하에 여러 증명을 하나의 증명으로 압축할 수 있어 증명이 더 작고 검증하기 쉬워집니다. 따라서 이 네 가지 요소를 결합하면 제로 지식 증명의 생성 효율성이 2년 전보다 세 배 향상되었습니다. 이것이 Scroll의 기원입니다.

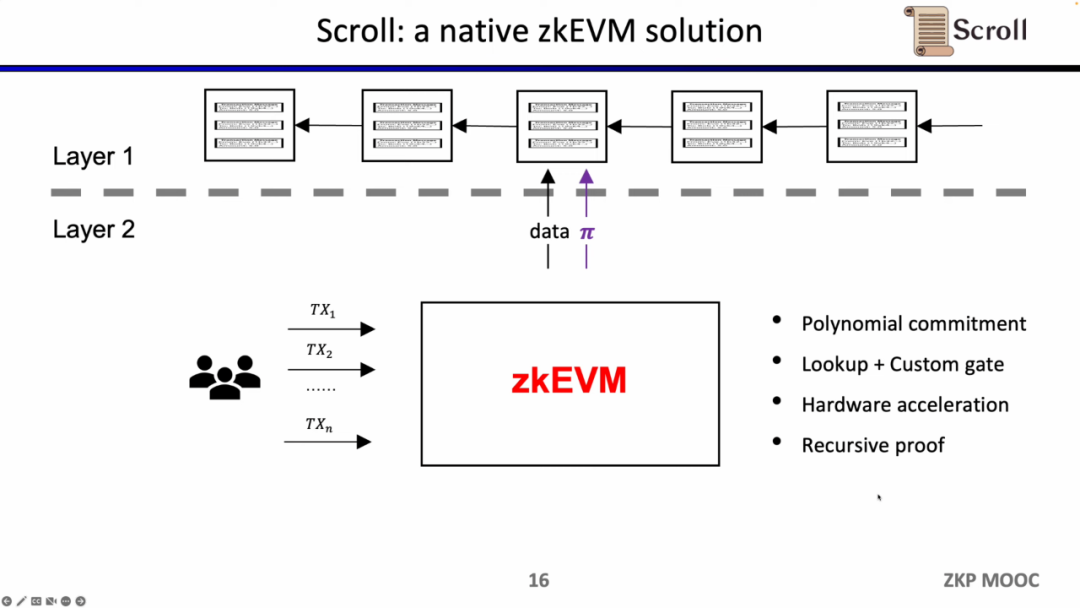
Justin Drake의 정의에 따르면, zkEVM은 세 가지 유형으로 나눌 수 있습니다. 첫 번째는 언어 수준의 호환성으로, 주된 이유는 EVM이 ZK를 위해 설계되지 않았기 때문에 ZK에 친화적이지 않은 많은 작업 코드가 있어 많은 추가 비용이 발생합니다. 따라서 Starkware와 zkSync는 Solidity 또는 Yul을 ZK 친화적인 컴파일러로 컴파일하는 언어 수준에서 선택합니다.

두 번째는 Scroll이 수행하는 바이트코드 수준의 호환성으로, EVM의 바이트코드 처리의 정확성을 직접 증명하며, 이더리움의 실행 환경을 직접 상속합니다. 여기서 할 수 있는 몇 가지 타협은 EVM과 다른 상태 루트를 사용하는 것, 예를 들어 ZK 친화적인 데이터 구조를 사용하는 것입니다. Hermez와 Consensys도 유사한 작업을 하고 있습니다.

세 번째는 합의 수준의 호환성으로, 여기서의 타협은 EVM을 변경하지 않을 뿐만 아니라 저장 구조 등 이더리움과 완전히 호환되도록 구현해야 하며, 그 대가는 더 긴 증명 시간이 필요하다는 것입니다. Scroll은 이더리움 재단의 PSE 팀과 협력하여 이더리움의 ZK화를 구현하고 있습니다.

0에서 1까지 zkEVM 구축하기

두 번째 부분에서 장예는 어떻게 0에서 시작하여 ZKVM을 구축하는지를 보여주었습니다.

전체 프로세스

먼저 ZKP의 프론트 엔드 부분에서, 당신은 수학적 산술화를 통해 계산을 표현해야 하며, 가장 일반적으로 사용되는 것은 선형 R1CS, Plonkish 및 AIR입니다. 산술화를 통해 제약을 얻은 후, ZKP의 백엔드에서 증명 알고리즘을 실행하여 계산의 정확성을 증명해야 합니다. 여기서는 가장 일반적으로 사용되는 다항식 상호작용 증명(Polynomial IOP) 및 다항식 약속 계획(PCS)을 나열합니다.

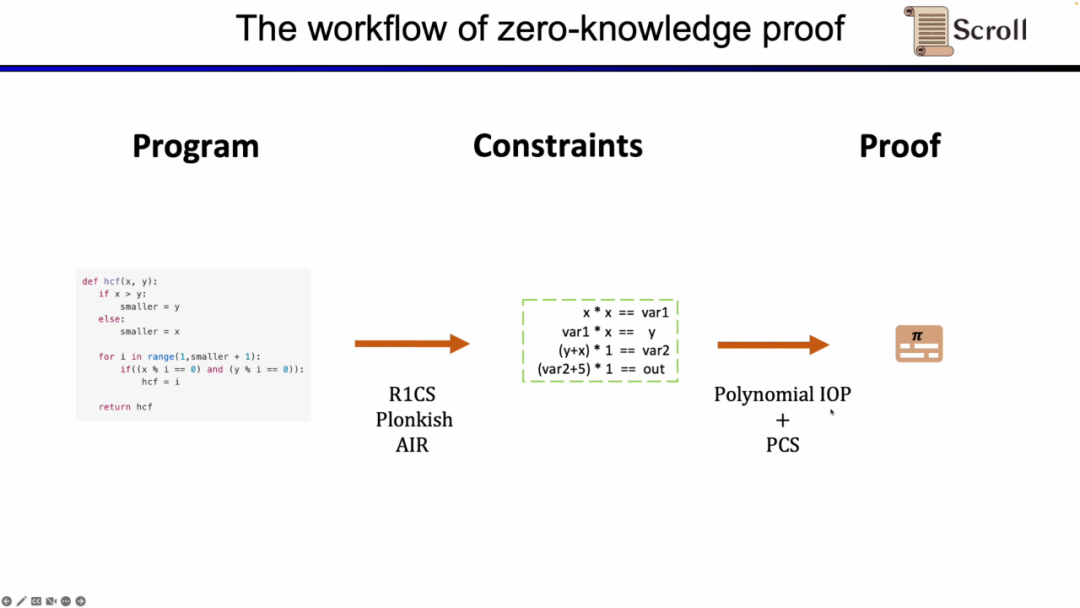
여기서 우리는 zkEVM을 증명해야 하며, Scroll은 Plonkish, Plonk IOP 및 KZG의 조합을 사용합니다.

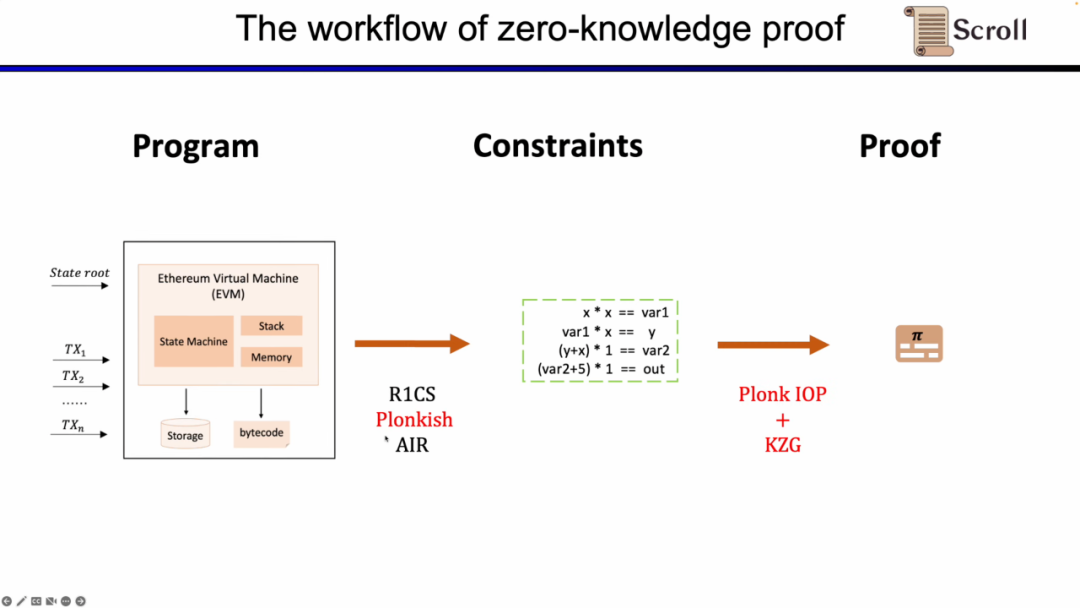
우리가 이 세 가지 솔루션을 사용하는 이유를 이해하기 위해, 우리는 가장 간단한 R1CS부터 시작합니다. R1CS의 제약은 선형 조합이 선형 조합에 곱해져 선형 결합과 같아야 합니다. 당신은 추가 비용 없이 어떤 변수의 선형 조합을 더할 수 있지만, 각 제약에서 차수는 최대 2입니다. 따라서 차수가 높은 연산에 대해서는 더 많은 제약이 필요합니다.

Plonkish에서는 모든 변수를 테이블에 입력해야 하며, 입력, 출력 및 중간 변수의 증인을 포함합니다. 그 위에 다양한 제약을 정의할 수 있습니다. Plonkish에서는 사용할 수 있는 세 가지 유형의 제약이 있습니다.

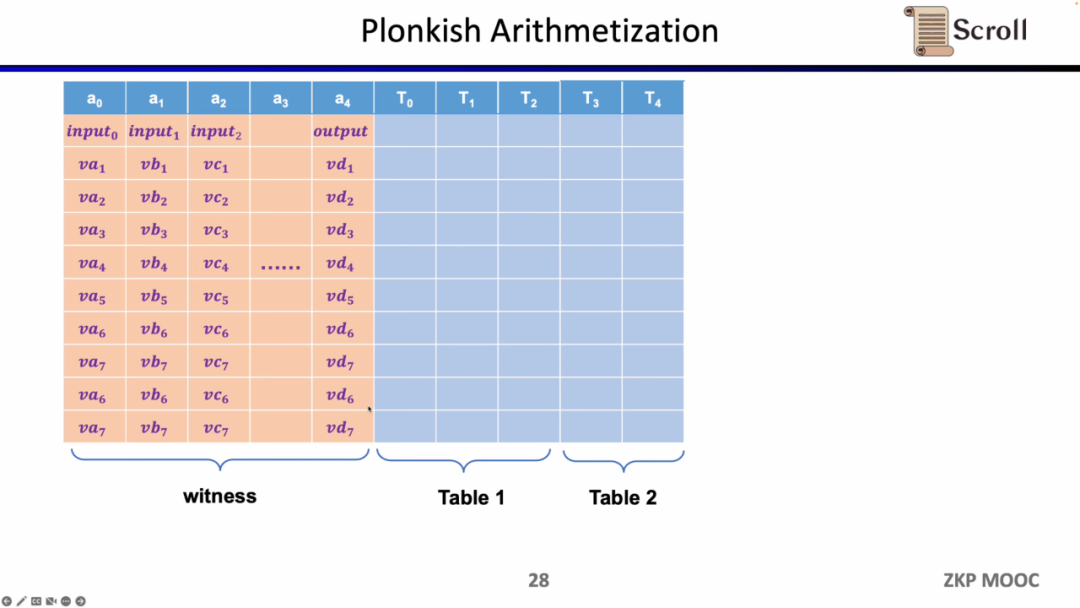
첫 번째 제약은 사용자 정의 게이트(Custom Gate)로, 서로 다른 셀 간의 다항식 제약 관계를 정의할 수 있습니다. 예를 들어 va3 * vb3 * vc3 - vb4 = 0입니다. R1CS에 비해 차수를 더 높일 수 있으며, 어떤 변수의 제약을 정의할 수 있고 매우 다양한 제약을 정의할 수 있습니다.

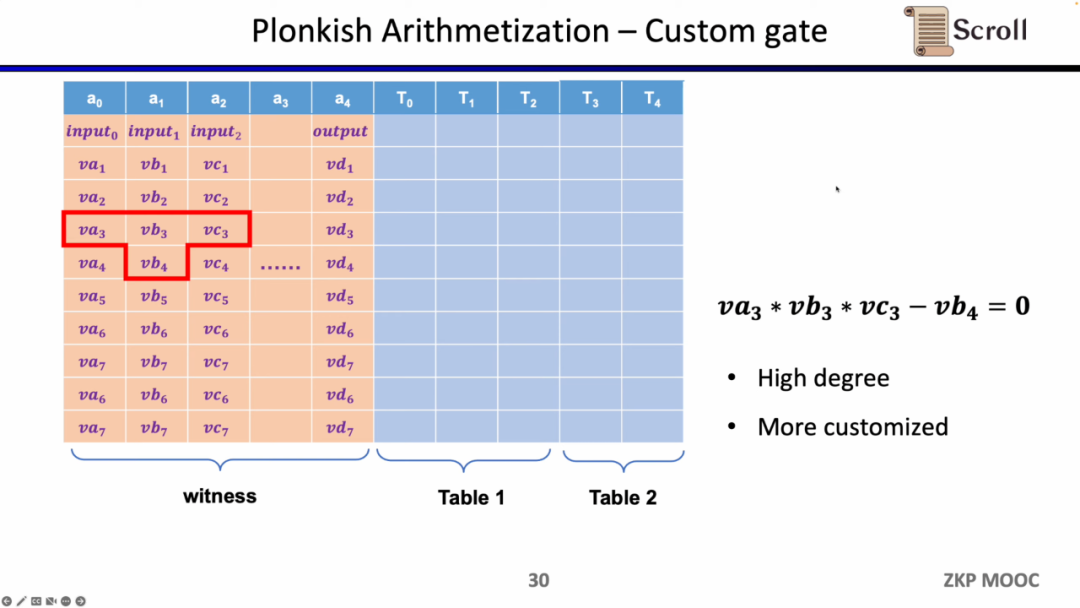
두 번째 제약은 순열(Permutation)로, 동등성 검사(equality checks)입니다. 서로 다른 셀의 동등성을 검사하는 데 사용되며, 일반적으로 연관 회로의 서로 다른 게이트에서 사용됩니다. 예를 들어 이전 게이트의 출력이 다음 게이트의 입력과 같음을 증명합니다.

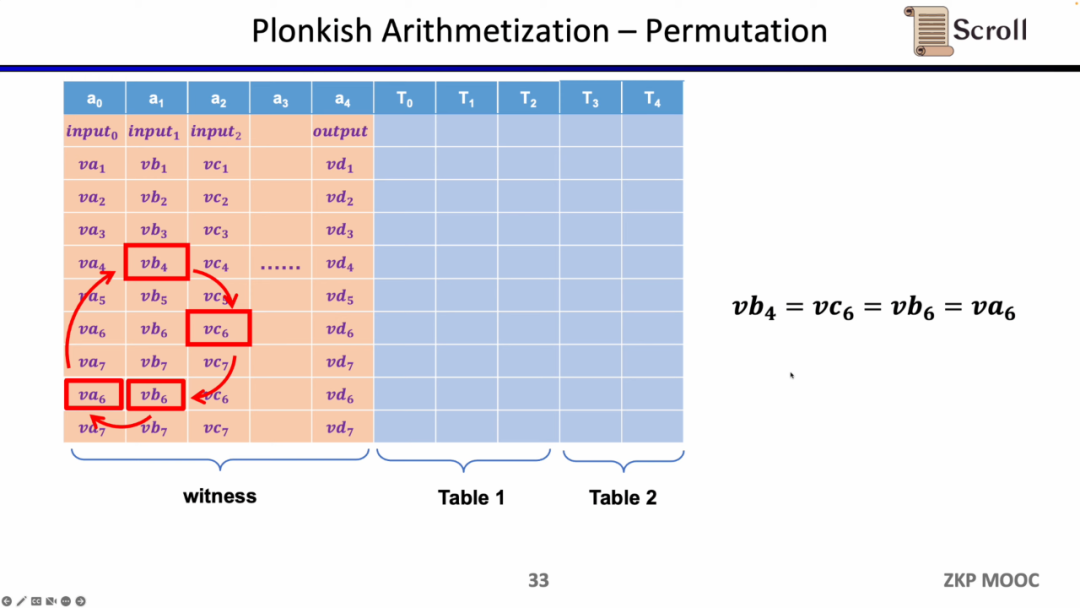
마지막 제약은 조회 테이블(Lookup Table)입니다. 우리는 조회 테이블을 변수 간의 관계로 이해할 수 있으며, 이 관계는 테이블로 표현될 수 있습니다. 예를 들어 vc7이 0-15 범위 내에 있음을 증명하고 싶다면, R1CS에서는 먼저 이 값을 4비트 이진수로 분해한 다음 각 비트가 0-1 범위 내에 있음을 증명해야 하며, 이는 네 개의 제약이 필요합니다. 그러나 Plonkish에서는 모든 가능한 범위를 동일한 열에 나열하고 vc7이 해당 열에 속함을 증명하기만 하면 되므로, 범위 증명에 매우 효율적이며, zkEVM에서 조회 테이블은 메모리 읽기 및 쓰기 증명에 매우 유용합니다.

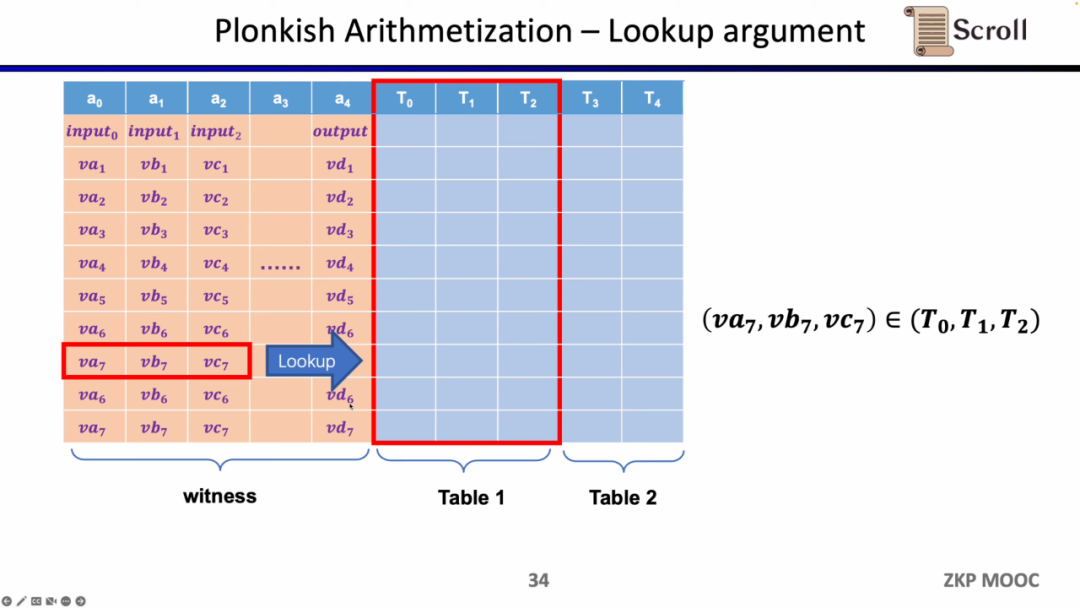
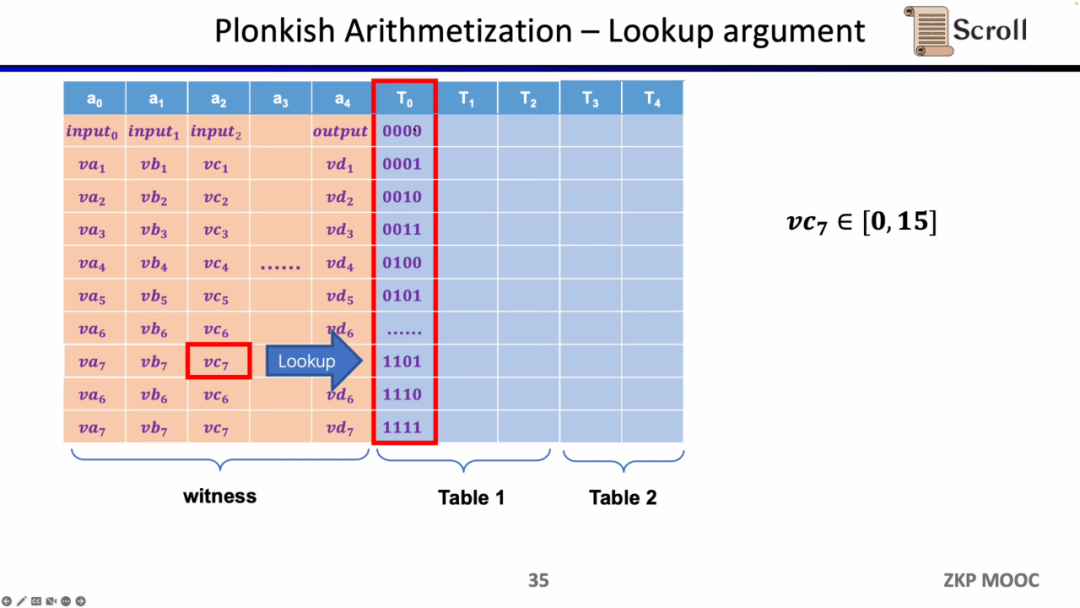
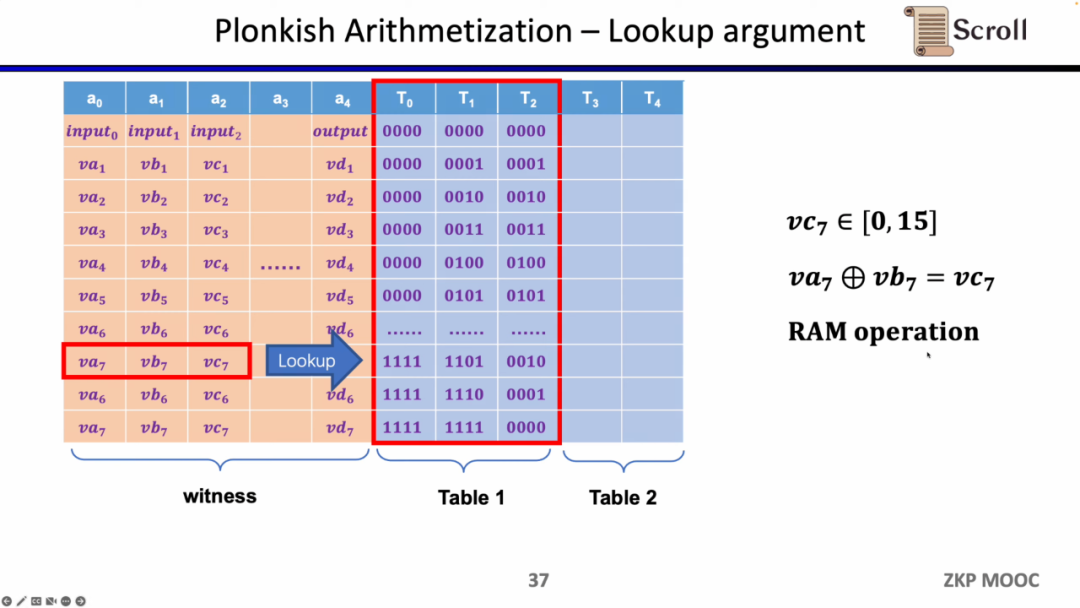
요약하자면, Plonkish는 사용자 정의 게이트, 동등성 검사 및 조회 테이블을 모두 지원하여 다양한 회로 요구를 매우 유연하게 충족할 수 있습니다. STARK와 간단히 비교하면, STARK에서는 각 행이 하나의 제약이며, 제약은 행 간의 상태 전환을 나타내야 하지만, Plonkish의 사용자 정의 제약은 명백히 더 높은 유연성을 제공합니다.

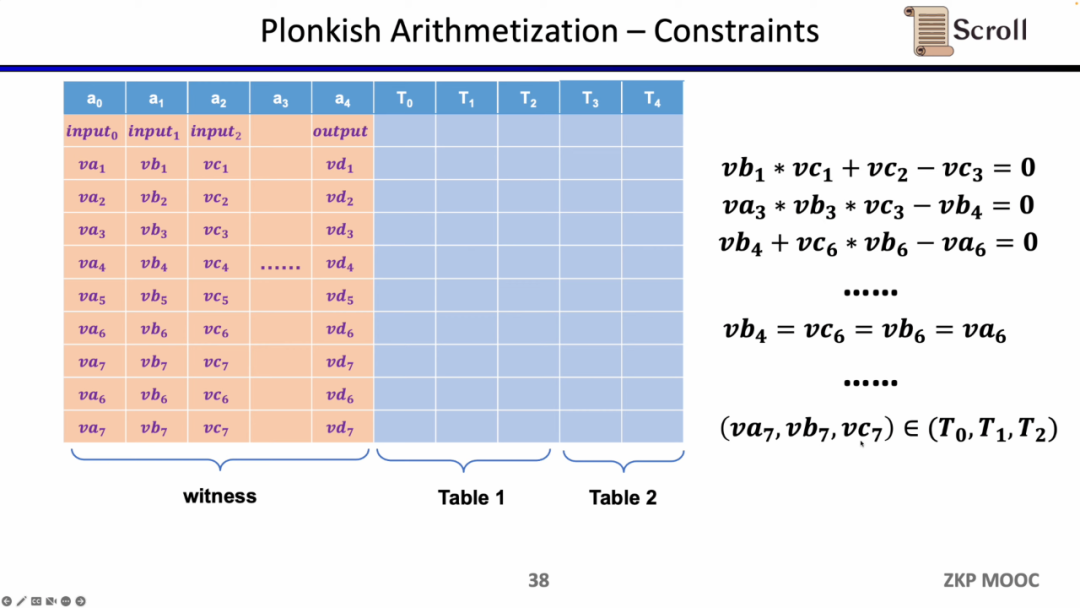
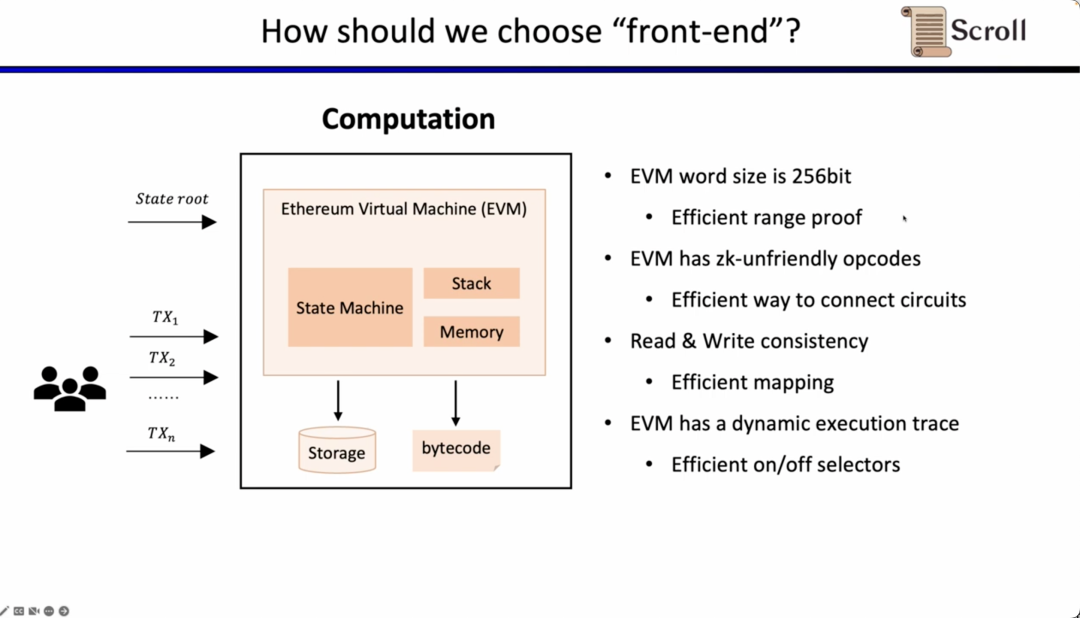
현재 문제는 zkEVM에서 프론트 엔드를 어떻게 선택할 것인가입니다. zkEVM에는 주로 네 가지 도전 과제가 있습니다. 첫 번째 도전 과제는 EVM의 필드가 256비트라는 것입니다. 이는 변수를 효율적으로 범위 제약을 적용해야 함을 의미합니다. 두 번째 도전 과제는 EVM에 ZK에 친화적이지 않은 많은 작업 코드가 있어 이러한 작업 코드를 증명하기 위해 매우 대규모의 제약이 필요하다는 것입니다. 예를 들어 Keccak-256입니다. 세 번째 도전 과제는 메모리 읽기 및 쓰기 문제로, 읽은 것과 이전에 쓴 것이 일치함을 증명하기 위해 유효한 매핑이 필요합니다. 네 번째 도전 과제는 EVM의 실행 추적이 동적으로 변화하므로, 서로 다른 실행 추적에 맞게 사용자 정의 게이트가 필요하다는 것입니다. 이러한 이유로 우리는 Plonkish를 선택했습니다.

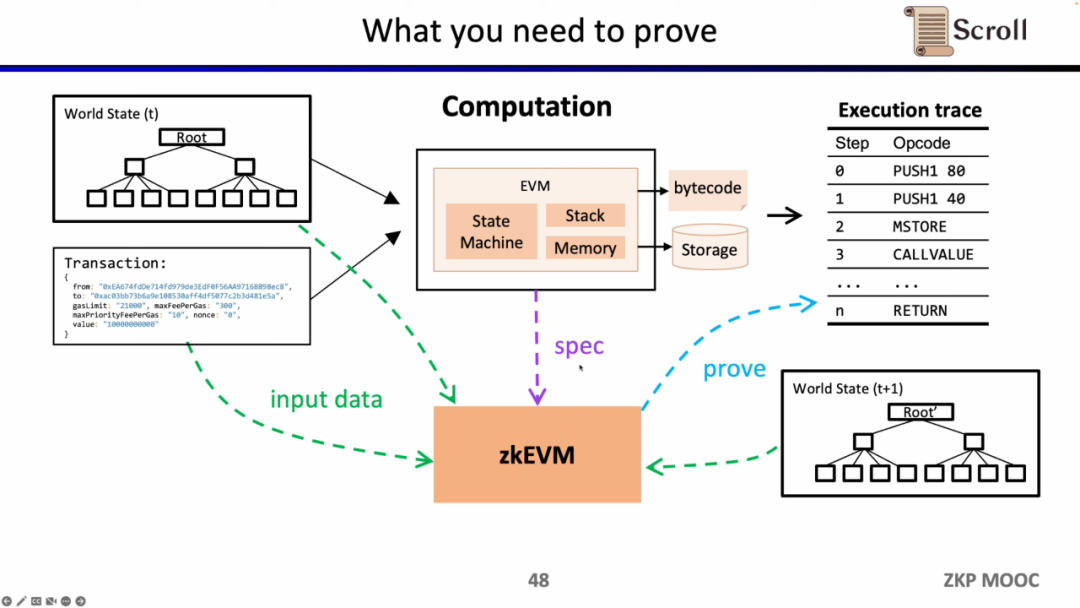
다음으로, zkEVM의 전체 프로세스를 살펴보겠습니다. 초기 전역 상태 트리를 기반으로 새로운 거래가 들어오면 EVM은 저장소와 호출된 계약의 바이트코드를 읽고 거래에 따라 PUSH, PUSH, STORE, CALLVALUE와 같은 실행 추적을 생성한 다음, 전역 상태를 업데이트하여 거래 후 전역 상태 트리를 얻습니다. zkEVM은 초기 전역 상태 트리, 거래 자체 및 거래 후 전역 상태 트리를 입력으로 사용하여 EVM의 규격에 따라 실행 추적의 실행 정확성을 증명합니다.

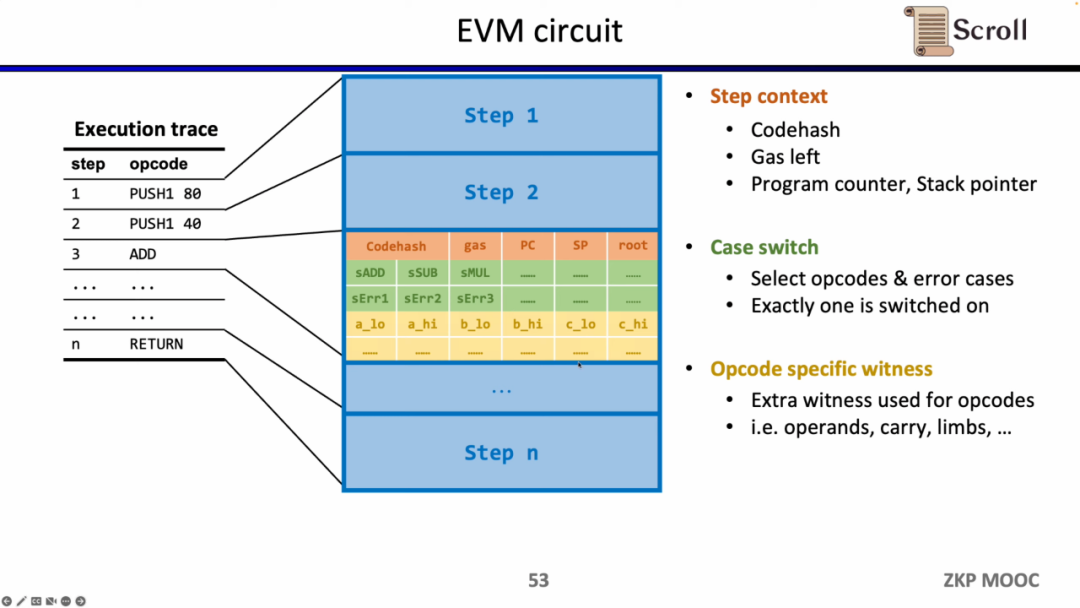
EVM 회로 세부 사항을 깊이 살펴보면, 각 실행 추적 단계에는 해당하는 회로 제약이 있습니다. 구체적으로 각 단계의 회로 제약은 Step Context, Case Switch, Opcode Specific Witness를 포함합니다. Step Context는 실행 추적에 해당하는 codehash, 남은 gas 및 카운터를 포함합니다. Case Switch는 모든 작업 코드, 모든 오류 상황 및 해당 단계의 관련 작업을 포함합니다. Opcode Specific Witness는 작업 코드에 필요한 추가 증인, 예를 들어 연산자 등을 포함합니다.

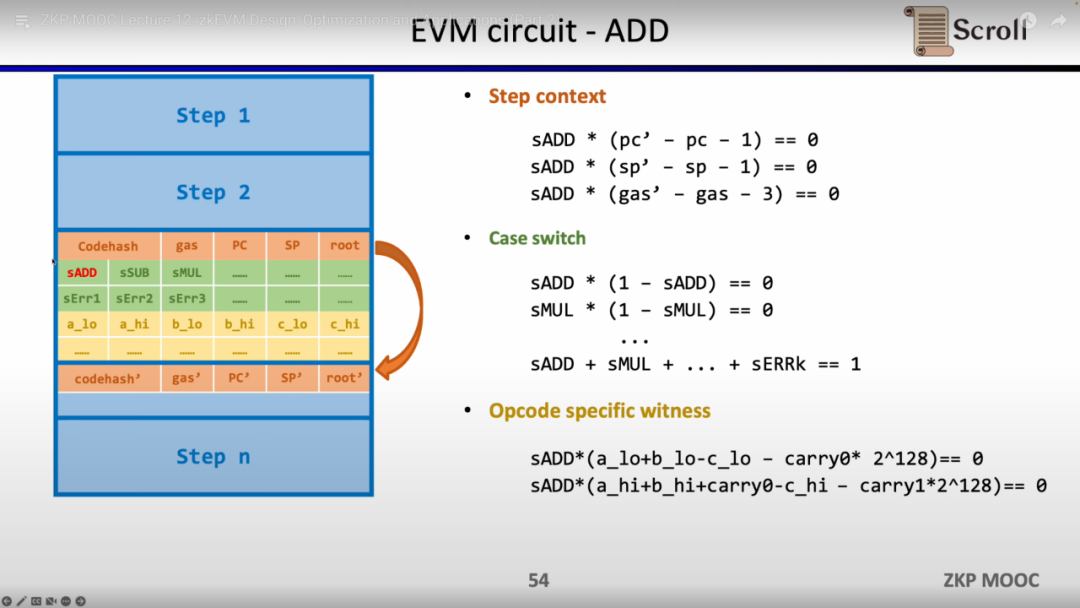
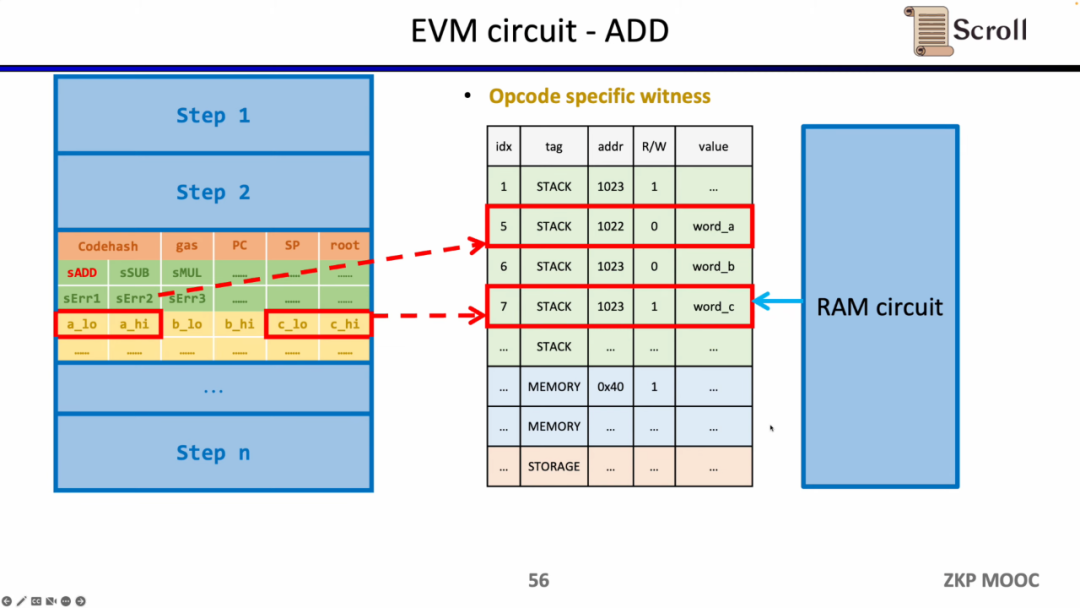
간단한 덧셈의 예를 들어보면, 덧셈 작업 코드의 제어 변수를 sADD로 설정하여 1로 설정하고, 다른 작업 코드 제어 변수는 모두 0으로 설정해야 합니다. Step Context에서는 gas' - gas - 3 = 0을 설정하여 소비된 gas가 3과 같도록 제약을 설정하고, 마찬가지로 카운터와 스택 포인터가 해당 단계 후에 1씩 증가하도록 제약을 설정합니다. Case Switch에서는 작업 코드 제어 변수가 1이 되도록 하여 해당 단계가 덧셈 작업임을 제약합니다. Opcode Specific Witness에서는 연산자의 실제 덧셈을 제약합니다.

또한 연산자가 메모리에서 읽히는 정확성을 보장하기 위해 추가적인 회로 제약이 필요합니다. 여기서 우리는 먼저 연산자가 메모리에 속함을 증명하기 위해 조회 테이블을 구축해야 합니다. 그리고 메모리 회로(RAM Circuit)를 통해 메모리 테이블의 정확성을 검증합니다.

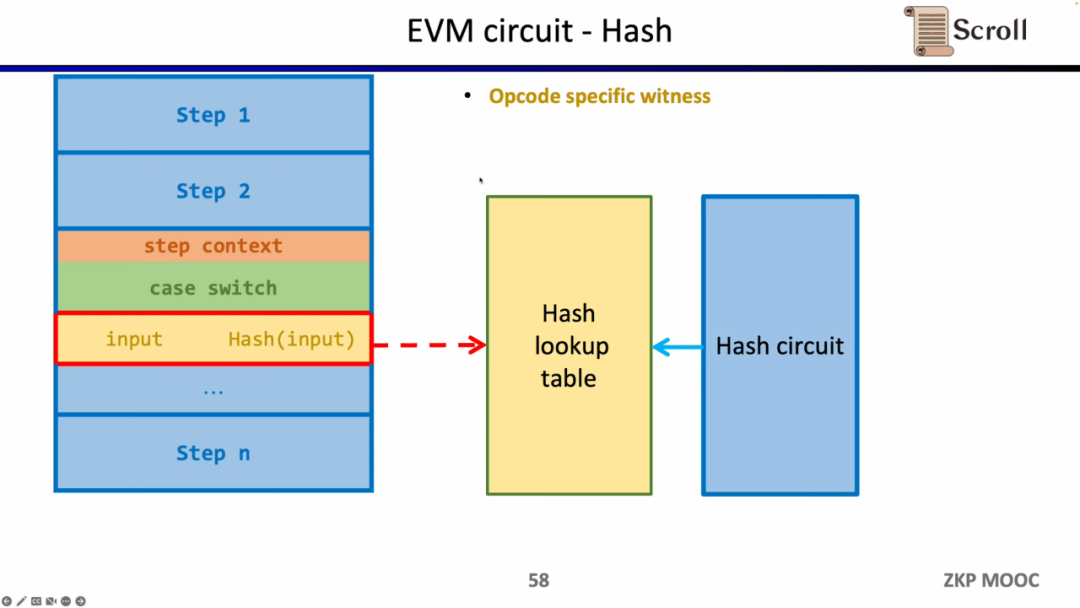
동일한 방법은 ZK에 친화적이지 않은 해시 함수에도 적용할 수 있으며, 해시 함수의 조회 테이블을 구축하고 실행 추적의 해시 입력과 출력을 조회 테이블에 매핑하여 추가 해시 회로(Hash Circuit)를 사용하여 해시 조회 테이블의 정확성을 검증합니다.

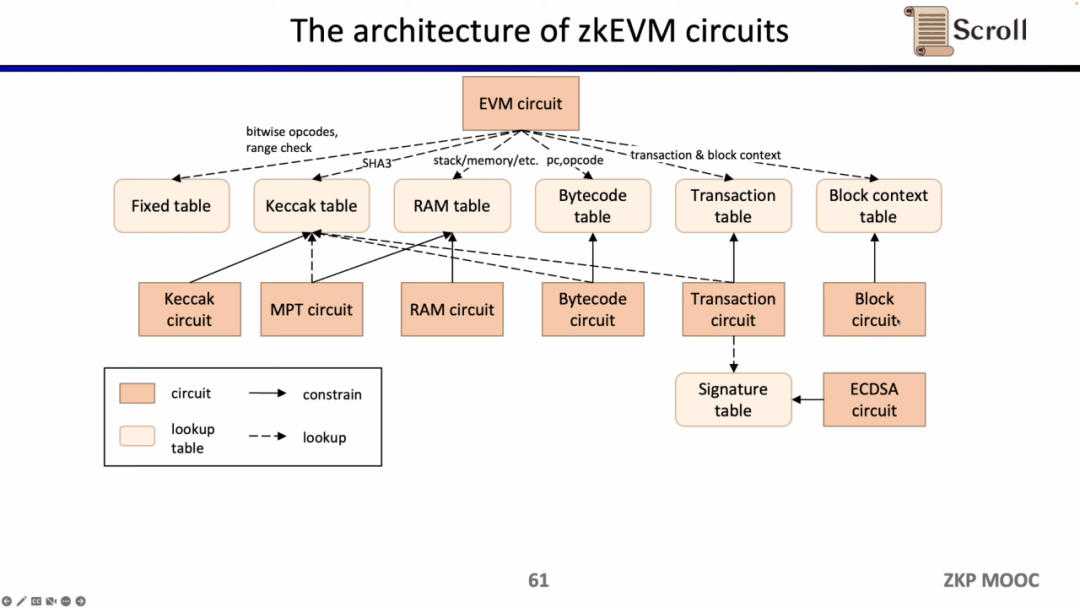
이제 zkEVM의 회로 아키텍처를 살펴보겠습니다. 핵심 EVM 회로는 실행 추적의 각 단계의 정확성을 제약하는 데 사용되며, 일부 EVM 회로 제약이 어려운 곳에서는 조회 테이블을 매핑합니다. 여기에는 Fixed Table, Keccak Table, RAM Table, Bytecode, Transaction, Block Context가 포함되며, 이러한 조회 테이블을 제약하기 위해 별도의 회로를 사용합니다. 예를 들어 Keccak 회로는 Keccak 테이블을 제약하는 데 사용됩니다.

요약하자면, zkEVM의 전체 작업 흐름은 아래 그림과 같습니다.

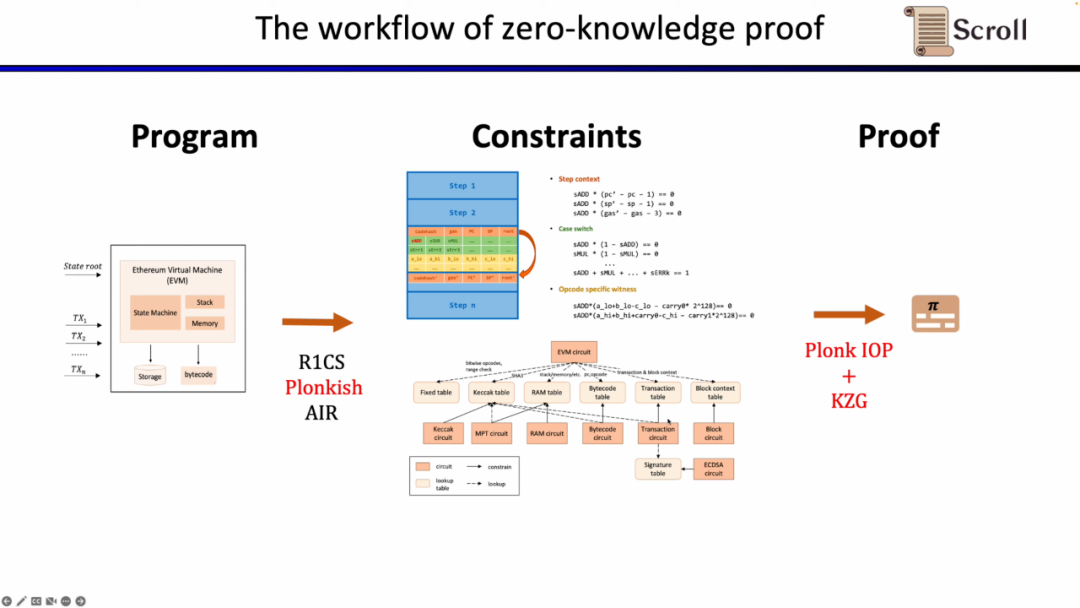
증명 시스템

L1에서 위의 EVM 회로, 메모리 회로, 저장 회로 등을 직접 검증하는 것은 비용이 매우 큽니다. Scroll의 증명 시스템은 두 층 구조를 채택하고 있습니다.

첫 번째 층은 EVM 자체를 직접 증명하는 역할을 하며, 증명을 생성하기 위해 많은 계산이 필요합니다. 따라서 첫 번째 층 증명 시스템은 사용자 정의 게이트와 조회 테이블을 지원해야 하며, 하드웨어 가속에 친화적이어야 하고, 낮은 피크 메모리에서 병렬로 계산을 생성하며, 검증 회로 규모가 작아 빠르게 검증할 수 있어야 합니다. 유망한 선택 사항으로는 Plonky2, Starky, eSTARK가 있으며, 이들은 프론트 엔드에서 기본적으로 Plonk를 사용하지만, 백엔드에서는 FRI를 사용할 수 있으며, 모두 위의 네 가지 특성을 충족합니다. 또 다른 선택 사항으로는 Zcash가 개발한 Halo2와 KZG 버전의 Halo2가 있습니다.

또한 최근 FFT를 제거한 HyperPlonk와 NOVA 증명 시스템과 같은 새로운 증명 시스템도 매우 유망합니다. 그러나 이들은 연구 중에 R1CS만 지원하며, 향후 Plonkish를 지원하고 실제로 적용된다면 매우 실용적이고 효율적일 것입니다.

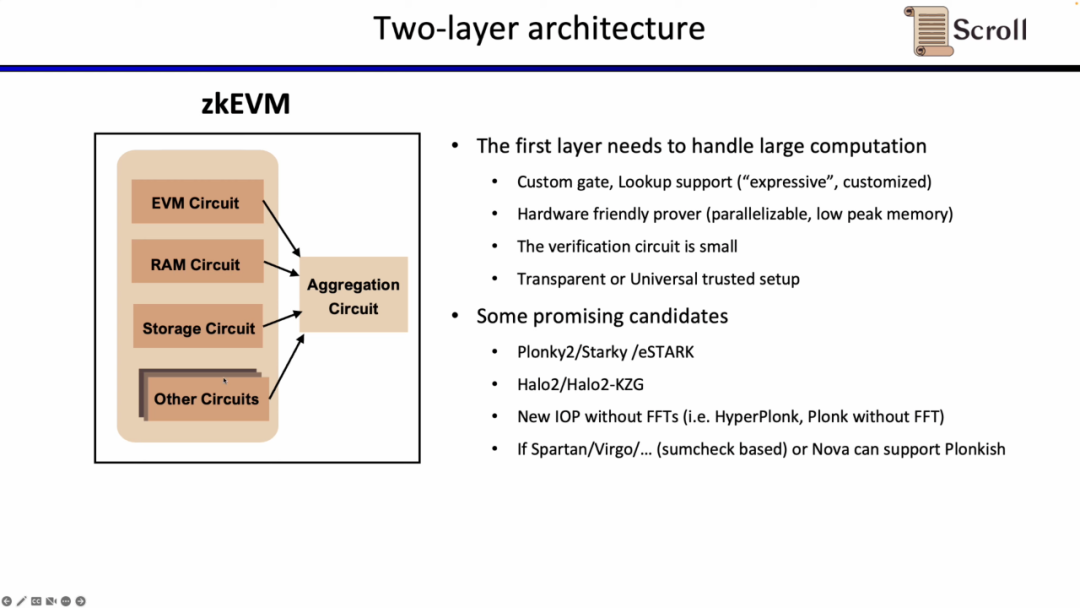
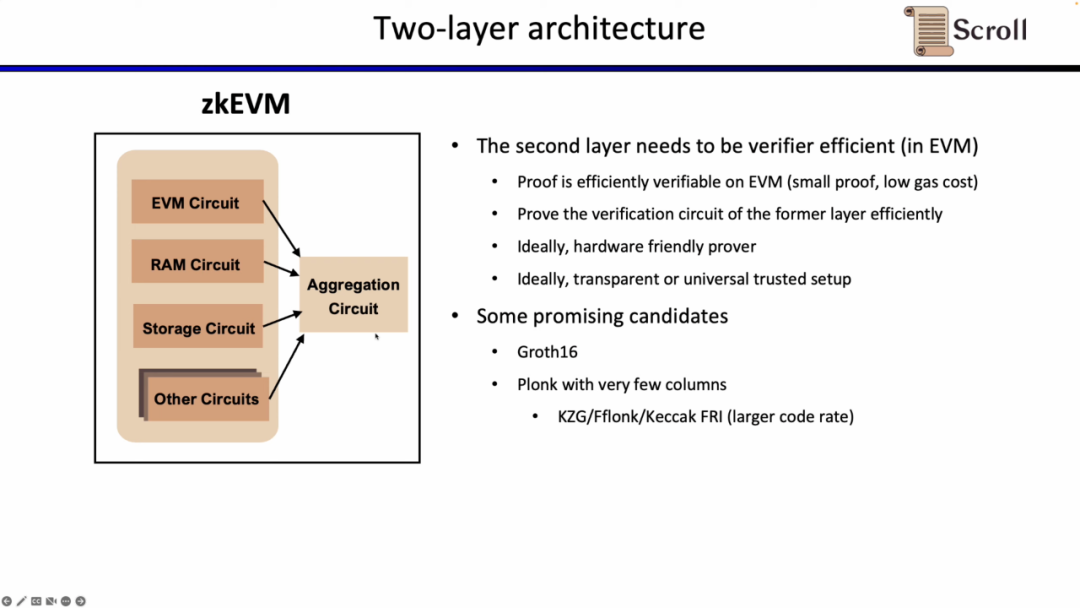
두 번째 층 증명 시스템은 첫 번째 층 증명의 정확성을 증명하는 데 사용되며, EVM에서 효율적으로 검증할 수 있어야 합니다. 이상적으로는 하드웨어 가속에 친화적이어야 하며, 투명하거나 보편적인 설정을 지원해야 합니다. 유망한 선택 사항으로는 Groth16과 열 수가 적은 Plonkish 증명 시스템이 있습니다. Groth16은 현재 연구 중에서 증명 효율성이 매우 높은 대표적인 시스템이며, Plonkish 증명 시스템은 열 수가 적은 경우에도 높은 증명 효율성을 달성할 수 있습니다.

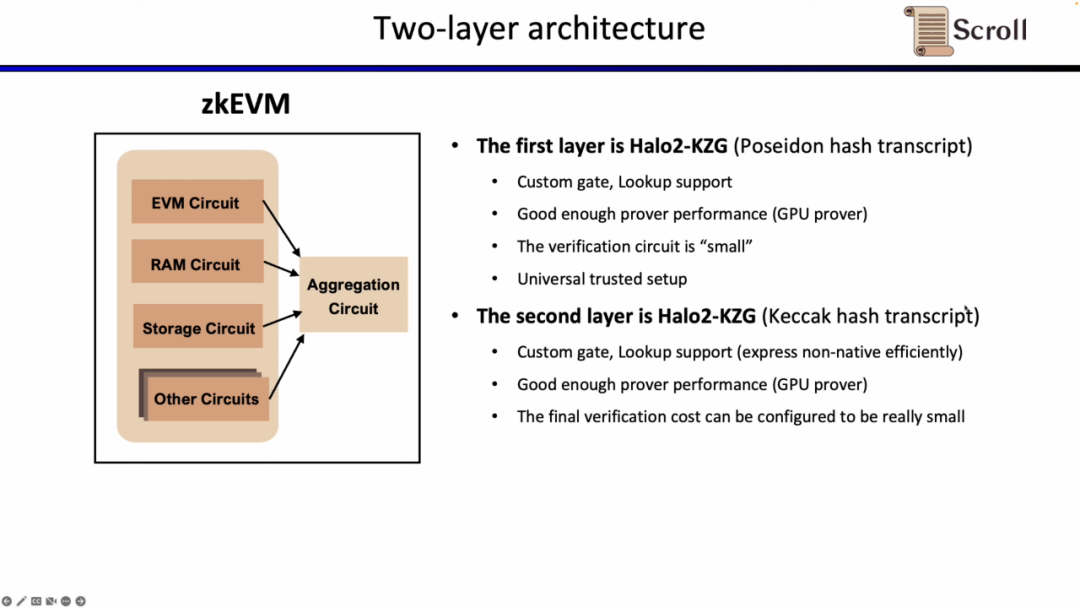
Scroll에서는 두 층 증명 시스템 모두 Halo2-KZG 증명 시스템을 채택하고 있습니다. Halo2-KZG는 사용자 정의 게이트와 조회 테이블을 지원하며, GPU 하드웨어 가속 하에서 성능이 우수하고, 검증 회로 규모가 작아 빠르게 검증할 수 있습니다. 차이점은 첫 번째 층 증명 시스템에서 Poseidon 해시를 사용하여 증명 효율성을 더욱 높였고, 두 번째 층 증명 시스템은 이더리움에서 직접 검증하므로 여전히 Keccak 해시를 사용하고 있습니다. Scroll은 또한 두 번째 층 증명 시스템에서 생성된 집합 증명을 추가로 집합하기 위해 다층 증명 시스템의 가능성을 탐색하고 있습니다.

현재 구현에서 Scroll의 첫 번째 층 증명 시스템 EVM 회로는 116열, 2496개의 사용자 정의 게이트, 50개의 조회 테이블, 최대 차수는 9이며, 1M Gas에서 2^18행이 필요합니다. 두 번째 층 증명 시스템의 집합 회로는 23열, 1개의 사용자 정의 게이트, 7개의 조회 테이블, 최대 차수는 5이며, EVM 회로, 메모리 회로, 저장 회로를 집합하기 위해 2^25행이 필요합니다.

Scroll은 GPU 하드웨어 가속 측면에서도 많은 연구와 최적화를 진행했습니다. EVM 회로의 경우, 최적화된 GPU 증명자는 단 30초가 소요되며, CPU 증명자에 비해 9배의 효율성을 향상시켰습니다. 집합 회로의 경우, 최적화된 GPU 증명자는 단 149초가 소요되며, CPU에 비해 15배의 효율성을 향상시켰습니다. 현재 최적화 조건 하에서 1M Gas의 첫 번째 층 증명 시스템은 약 2분, 두 번째 층 증명 시스템은 약 3분이 소요됩니다.

흥미로운 연구 문제

세 번째 부분에서 장예는 Scroll이 zkEVM 구축 과정에서 직면한 흥미로운 연구 문제를 논의했습니다. 여기에는 프론트 엔드의 산술 회로에서 증명자의 구현까지 포함됩니다.

회로

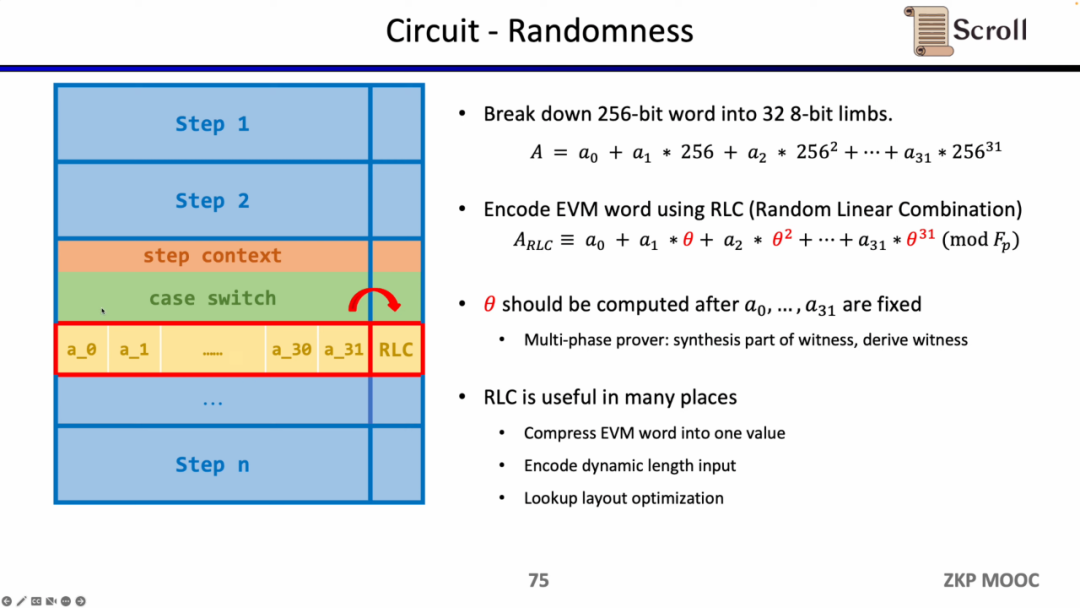
첫 번째는 회로의 무작위성입니다. EVM 필드가 256비트이기 때문에 이를 32개의 8비트 필드로 분할하여 범위 증명을 더 효율적으로 수행해야 합니다. 이후 우리는 무작위 선형 조합(Random Linear Combination, RLC) 방법을 사용하여 32개의 필드를 1개로 인코딩합니다. 이 필드만 검증하면 원래의 256비트 필드를 검증할 수 있습니다. 그러나 문제는 무작위 수의 생성이 필드를 분할한 후에 이루어져야 하므로 변조되지 않도록 보장해야 한다는 것입니다.

따라서 Scroll과 PSE 팀은 필드 분할 후 무작위 수를 사용하여 RLC를 생성하는 다단계 증명자 솔루션을 제안했습니다. 이 솔루션은 Challenge API에 캡슐화되어 있습니다. RLC는 zkEVM에서 여러 응용 시나리오가 있으며, EVM 필드를 하나의 필드로 압축하거나 가변 길이 입력을 암호화하거나 조회 테이블의 레이아웃을 최적화하는 데 사용될 수 있지만 여전히 해결해야 할 많은 개방형 문제가 있습니다.

회로 측면에서 두 번째 흥미로운 연구 문제는 회로 레이아웃입니다. Scroll의 프론트 엔드가 Plonkish를 채택한 이유는 EVM의 실행 추적이 동적으로 변화하기 때문에 다양한 제약과 변화하는 동등성 검사를 지원해야 하며, R1CS의 표준화된 게이트는 더 큰 회로 규모를 필요로 하기 때문입니다.

그러나 Scroll은 현재 2000개 이상의 사용자 정의 게이트를 사용하여 동적으로 변화하는 실행 추적을 충족하고 있으며, Opcode를 마이크로 Opcode로 분할하거나 동일한 테이블 내의 셀을 재사용하는 등 회로 레이아웃을 추가로 최적화하는 방법을 탐색하고 있습니다.

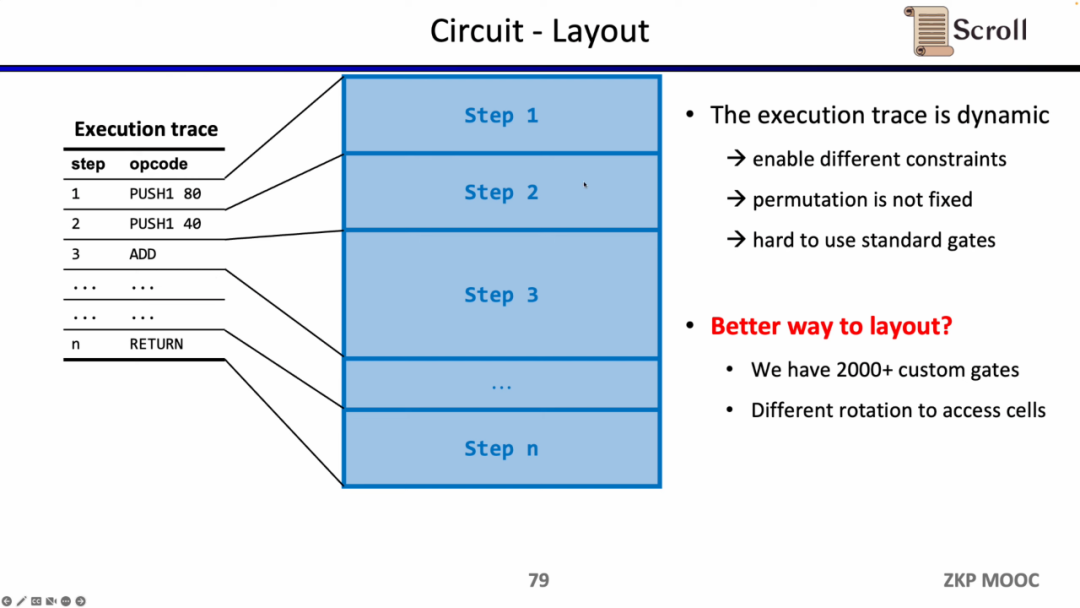
회로 측면에서 세 번째 흥미로운 연구 문제는 동적 규모입니다. 서로 다른 작업 코드의 회로 규모가 다르지만, 동적으로 변화하는 실행 추적을 충족하기 위해 각 단계의 작업 코드는 최대 회로 규모를 충족해야 하므로 실제로 추가 비용이 발생합니다. zkEVM이 동적으로 변화하는 실행 추적에 적응할 수 있다면 불필요한 비용을 절감할 수 있습니다.

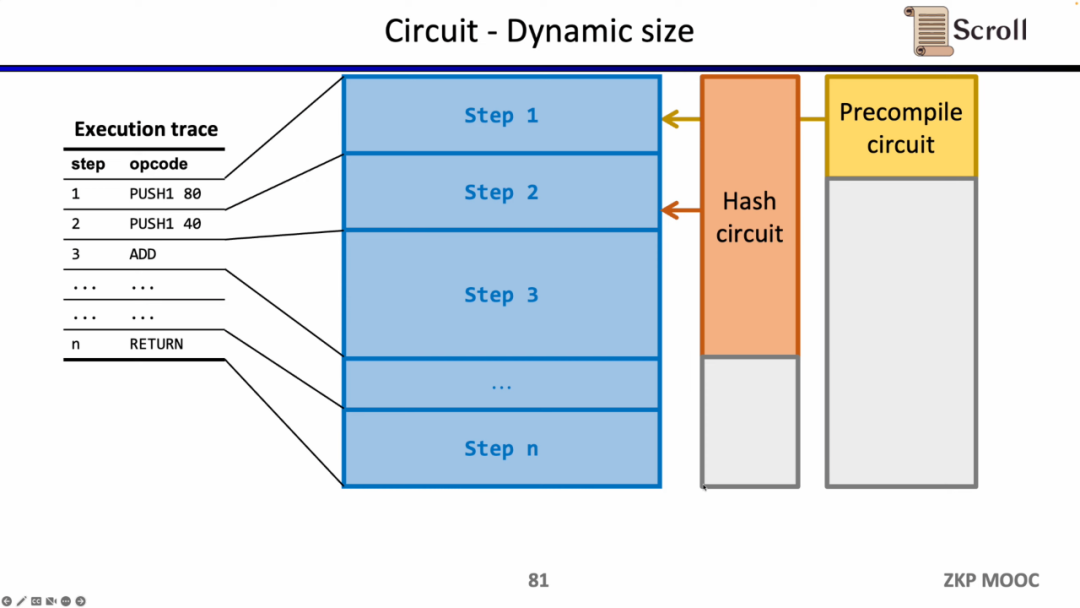
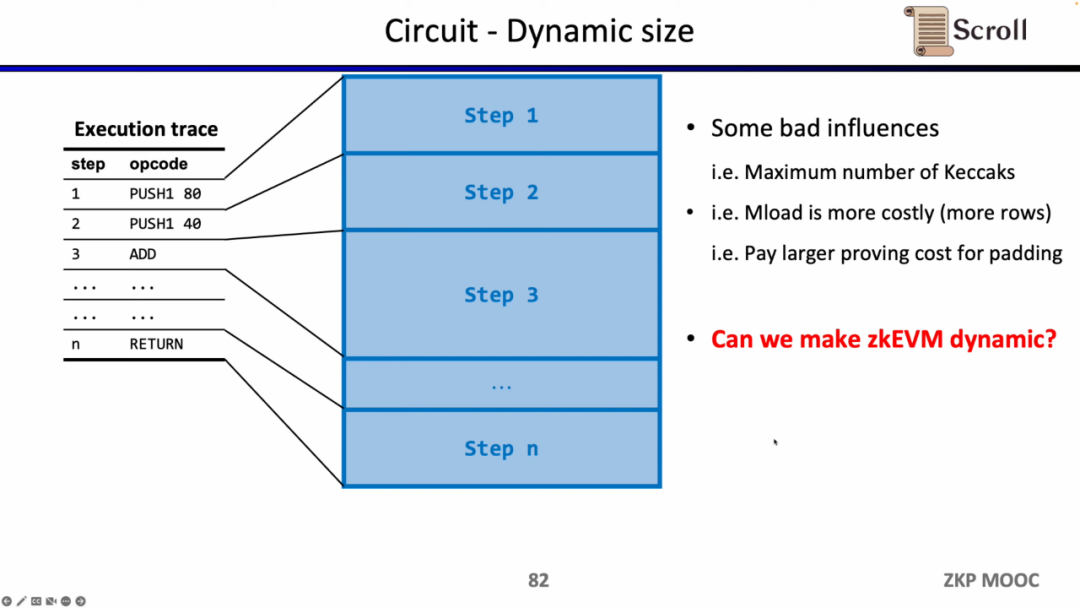
증명자

증명자 측면에서 Scroll은 GPU 가속에서 MSM과 NTT에 대한 많은 최적화를 진행했지만, 현재의 병목 현상은 증인 생성 및 데이터 복사로 이동했습니다. MSM과 NTT가 증명 시간의 80%를 차지한다고 가정할 때, 하드웨어 가속이 이 부분의 효율성을 몇 배 향상시킬 수 있지만, 원래 증인 생성 및 데이터 복사에 소요되는 20%의 증명 시간이 새로운 병목 현상이 됩니다. 증명자의 또 다른 문제는 많은 메모리가 필요하므로 더 저렴하고 탈중앙화된 하드웨어 솔루션을 탐색해야 한다는 것입니다.

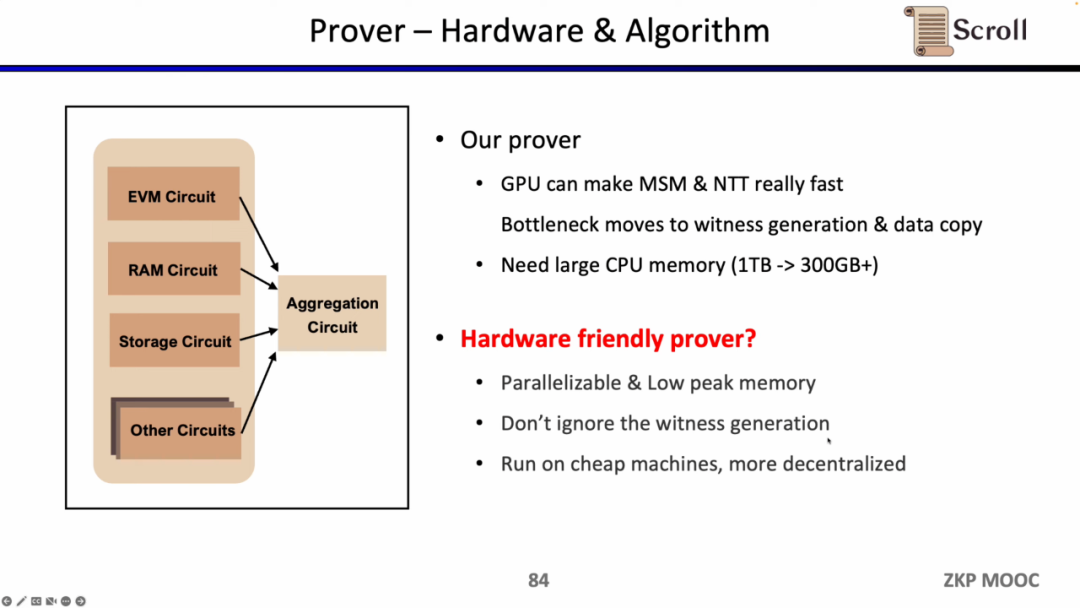
동시에 Scroll은 하드웨어 가속 및 증명 알고리즘 측면에서도 증명자의 효율성을 높이기 위해 탐색하고 있습니다. 현재 주요 방향은 더 작은 도메인으로 전환하는 것, 예를 들어 64비트 Goldilocks 도메인, 32비트 메르센 소수(Mersenne Prime) 등을 사용하는 것과, 타원 곡선(EC)을 기반으로 한 새로운 증명 시스템인 SuperNova를 고수하는 것입니다. 물론 다른 가능성 있는 경로도 있으며, 아이디어가 있는 분들은 Scroll과 직접 연락해 주시기 바랍니다.

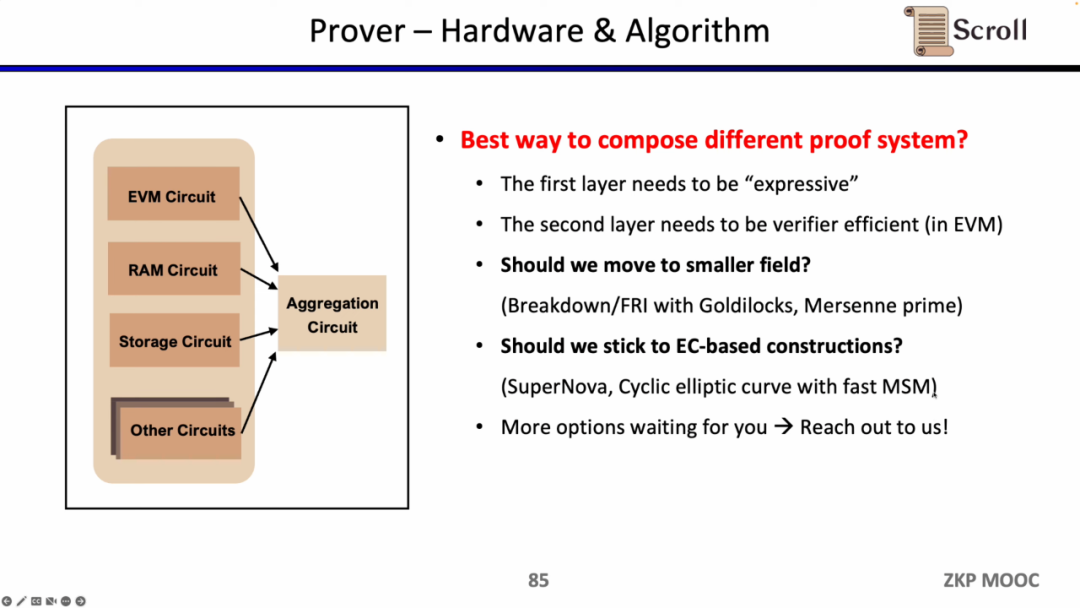
보안성

zkEVM을 구축할 때 보안성은 매우 중요합니다. PSE와 Scroll이 공동으로 구축한 zkEVM은 약 34,000줄의 코드로 구성되어 있으며, 소프트웨어 공학 관점에서 이러한 복잡한 코드베이스는 오랜 시간 동안 결함이 없을 수 없습니다. Scroll은 현재 업계 최고의 감사 회사들을 포함하여 많은 감사를 통해 zkEVM의 코드베이스를 검토하고 있습니다.

zkEVM을 사용하는 다른 응용 프로그램

네 번째 부분에서는 zkEVM을 사용하는 다른 응용 프로그램에 대해 논의합니다.

zkRollup 아키텍처에서 우리는 L1의 스마트 계약을 통해 L2에서 n개의 거래가 유효한지를 검증합니다.

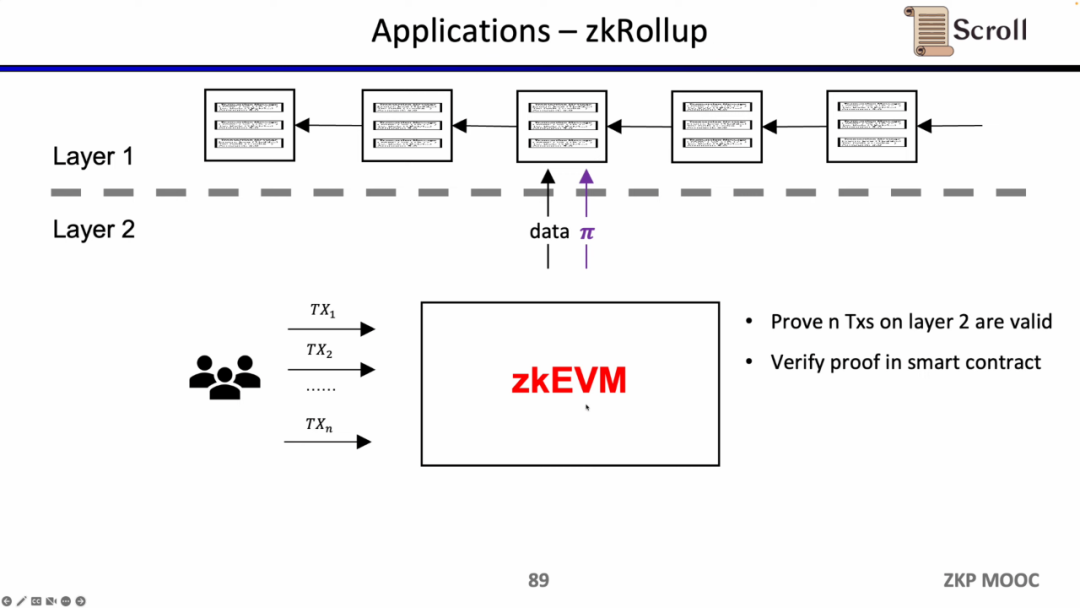
우리가 L1의 블록을 직접 검증한다면, L1의 노드는 거래를 반복 실행할 필요가 없으며, 각 블록 증명의 유효성만 검증하면 됩니다. 이러한 아키텍처 솔루션을 Enshrine Blockchain이라고 합니다. 현재 이더리움에서 직접 구현하는 것은 매우 어렵습니다. 왜냐하면 전체 이더리움 블록을 검증해야 하며, 여기에는 많은 서명을 검증해야 하므로 더 긴 증명 시간과 낮은 보안성을 초래하기 때문입니다. 물론 이미 다른 공공 블록체인에서도 재귀 증명을 통해 단일 증명을 사용하여 전체 블록체인을 검증하는 방법을 사용하고 있습니다. 예를 들어 Mina입니다.

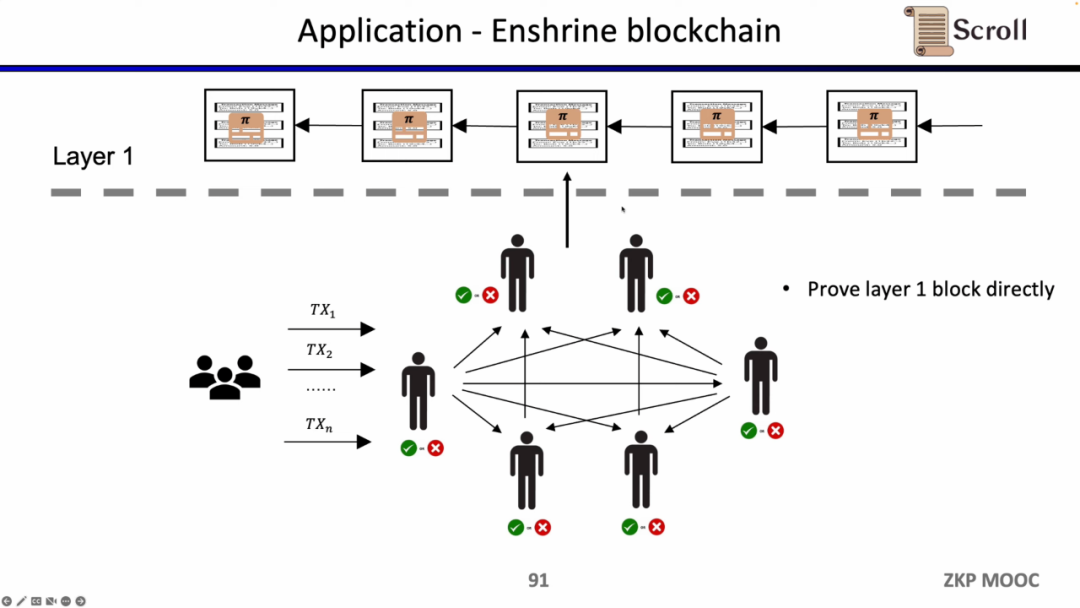
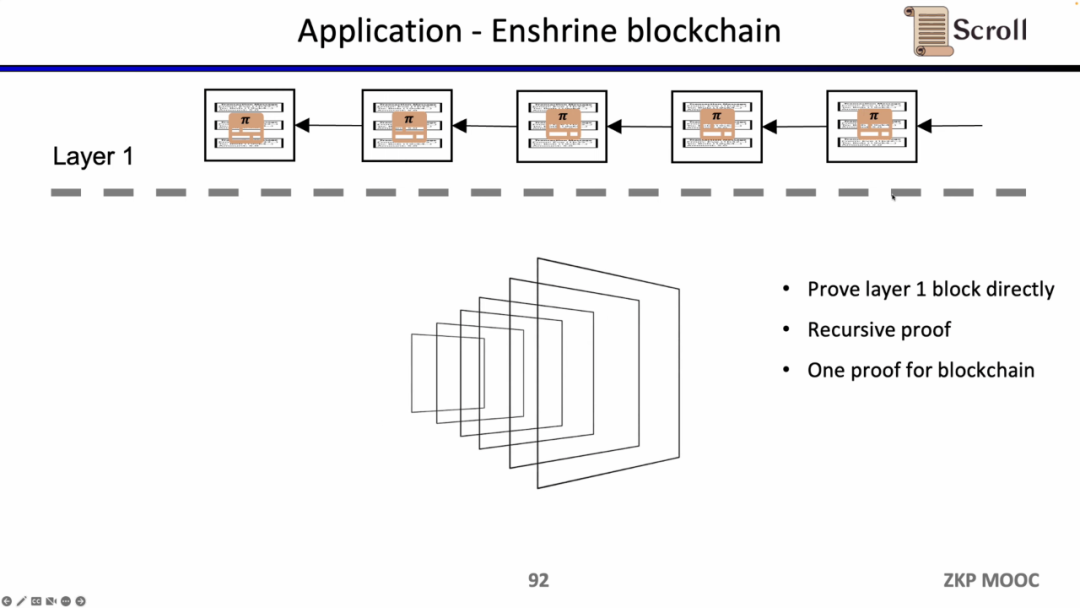
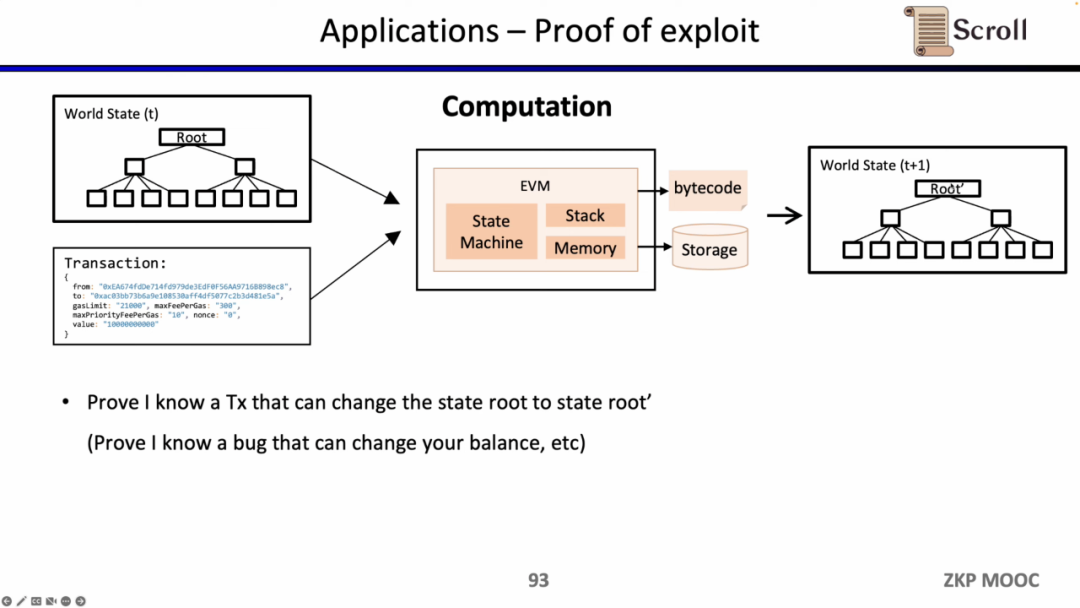
zkEVM은 상태 전환을 증명할 수 있기 때문에, 화이트 해커가 특정 스마트 계약의 취약점을 알고 있음을 증명하여 프로젝트 측에 보상을 요청하는 데 활용될 수 있습니다.

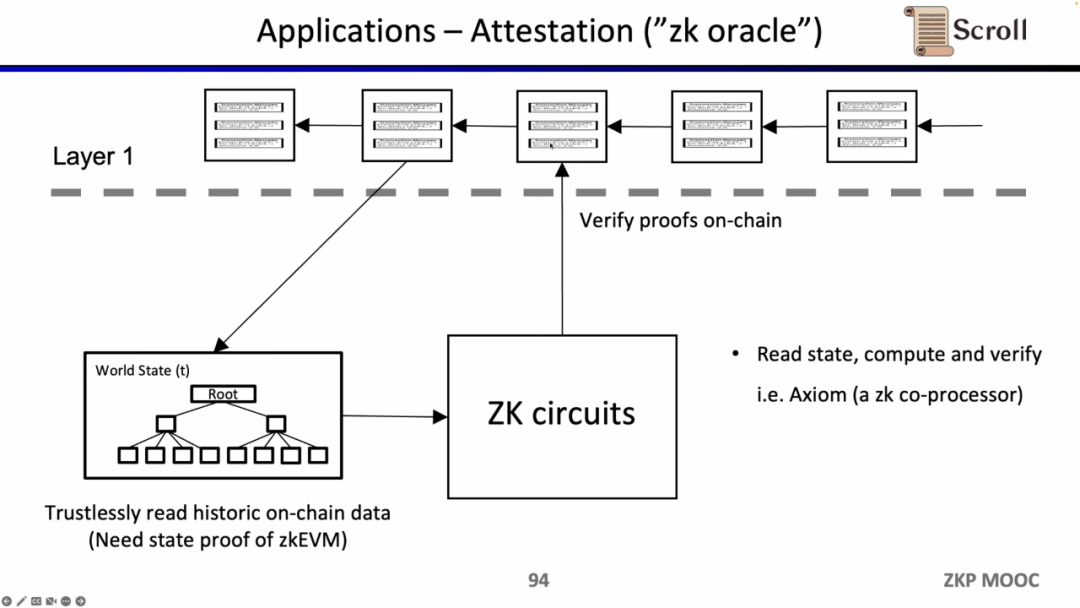
마지막 사용 사례는 제로 지식 증명을 통해 역사적 데이터에 대한 주장을 증명하는 것으로, 오라클로 사용됩니다. 현재 Axiom이 이와 관련된 제품을 개발하고 있습니다. 최근 ETHBeijing 해커톤에서 GasLockR 팀은 이 특성을 활용하여 역사적인 Gas 비용을 증명했습니다.

마지막으로, Scroll은 zkRollup의 이더리움 일반 확장 솔루션을 구축하고 있으며, 매우 진보된 산술 회로와 증명 시스템을 사용하고 있으며, 하드웨어 가속을 통해 빠른 검증기를 구축하여 증명 재귀를 수행하고 있습니다. 현재 Alpha 테스트넷이 이미 온라인 상태이며, 오랜 시간 동안 안정적으로 운영되고 있습니다.

물론 여전히 해결해야 할 흥미로운 문제들이 있으며, 프로토콜 설계 및 메커니즘 설계, 제로 지식 엔지니어링 및 실제 효율성 등이 포함됩니다. 여러분이 Scroll에 참여하여 함께 구축하기를 환영합니다!