Paradigm research partners propose a new NFT primitive, Mortys, to better achieve NFT fragmentation applications

Author: Dave White, Blockchain Investment Firm Paradigm

Summary

This article introduces a new NFT primitive: Martingale shares, or "Mortys." (Note: Martingale is a concept in probability theory.)

Mortys are synthetic representations of fractional ownership in an NFT category.

They do not require buyouts or oracle mechanisms, but instead rely on a random Martingale settlement process.

Mortys are highly speculative and should be considered something between protocol design and thought experiment.

Motivation

Imagine Alice owns an Ocelot from the Awful Hot Ocelots series.

When she bought this Ocelot, it was not worth much. However, the project has since taken off, and she wants to gain some liquidity and reduce her price exposure.

She does not want to sell her Ocelot directly and has set it as her Twitter profile picture, being very attached to it. Ideally, she just wants to sell half of it.

Challenges of NFT Fractionalization

If she wanted to sell half a cookie, she could simply sell half. If she wanted to sell 50% of a business, she could sell 50% of the shares representing its cash flow.

However, her Ocelot NFT is not naturally divisible and does not generate any cash flow. How can it be split in an economically meaningful way?

Fractional

fractional.art would allow Alice to fractionalize her Ocelot by selling tokens and extracting 50% of the proceeds from its eventual future sale. This means Fractional must ensure that future sales will be fair and will actually happen. Therefore, the protocol implements a buyout mechanism that allows interested buyers to initiate an auction for this Ocelot at any time.

This works very well for famous and unique NFTs with a lot of market interest. However, for more ordinary NFTs like Alice's Ocelot, it becomes a bit tricky.

The fractional shares of her Ocelot would be a brand new token, and Alice would have to create a new market for them somewhere like Uniswap. Given that many Ocelots have already been fractionalized, she doubts it would be easy to attract enough attention to sell her shares at a reasonable price.

Similarly, if someone later initiates a buyout auction for her Ocelot, it may not attract as much attention or liquidity, potentially leading to a sale at an unfavorable price for Alice.

Floor Perps

Alice could also mint some Floor Perps using her Ocelot, which are derivative synthetics that track the floor price of Ocelots using a funding rate mechanism and an oracle for the floor price.

However, her Ocelot is worth more than the floor price because it has the relatively sought-after wizard hat attribute.

In theory, she could create a floor perp to track the floor price of Wizard Hat Ocelots specifically, but this would require defining an oracle for the Wizard Hat Ocelot floor. Since there are only 200 Ocelots with the wizard hat attribute, any such oracle could be inaccurate and susceptible to manipulation.

Lottery-style Fractionalization

In a recent blog post, Vitalik Buterin provided a possible solution: Alice could sell fractions in the form of a lottery.

For example, suppose Alice's Ocelot is worth 10 ETH.

If she sells half of the Ocelot as a lottery to Bob, he would give her 5 ETH, and she would give him a 50% chance of winning the Ocelot by flipping a coin. If it lands heads, Alice gets the Ocelot back. If it lands tails, Bob gets the Ocelot.

Similarly, if Alice sells 10% of her Ocelot to Bob, he could give her 1 ETH, and they could roll a 10-sided die. If it lands on 1, Bob gets the Ocelot; if it lands on 2 to 9, Alice gets it.

The benefit of this arrangement is that it is entirely fair: the amount of ETH Bob pays is exactly equal to the expected value of the lottery ticket he receives. There are no chaotic liquidity dynamics around potential buyouts, nor are there concerns about the validity of oracle prices. If Bob buys 10% of the Ocelot, he has a 10% chance of getting it.

However, Alice may still be unsatisfied with this transaction. After all, she loves her Ocelot not just for its cash value. Here, she has a 10% chance of losing it immediately.

Moreover, lottery-style fractionalization does nothing to help Alice find liquidity or a fair price. In this example, we assume Alice and Bob agree that her Ocelot is worth 10 ETH. In reality, this is unlikely to be true, and Alice may have to hold an auction or negotiate privately with Bob to set a price.

Martingale Fractionalization

Martingale fractionalization addresses these issues while maintaining the perfect mathematical fairness of lottery fractionalization.

Like lottery fractionalization, Martingale fractionalization relies on randomness to determine ownership: Alice sells 50% of her Ocelot in the form of Martingale Shares or Mortys.

Over time, her remaining ownership will randomly contract and expand in a process called Martingale, meaning each step is fair. The process ends when her ownership drops to 0% or returns to 100%. Since this settlement occurs over time, these shares can be traded on markets like Uniswap, facilitating liquidity and price discovery.

At any time, Alice can replace the Ocelot she used as collateral with any other wizard hat Ocelot. This means Mortys do not represent a fraction of her specific Ocelot but rather a fraction of the cheapest delivery or floor price Ocelots in their category. This feature, along with Alice's ability to repurchase Wizard Hat Ocelot Mortys on the open market, allows her to reclaim her Ocelot in case luck is not on her side.

Mechanism Details

Opening a Vault

Alice opens a new Wizard Hat Ocelot Vault using her wizard hat Ocelot as collateral. The initial balance of the Vault is 100 Wizard Hat Ocelot Mortys.

As mentioned, Alice can replace the wizard hat Ocelot she used as collateral with any other wizard hat Ocelot at any time.

Morty Category

Alice's Vault and Mortys belong to the wizard hat Ocelot category, meaning they can only be created with wizard hat Ocelots. All Mortys in a given category are interchangeable. This is similar to Maker, where all DAI are interchangeable, even if created by different people in different Vaults with different collateral.

Alice could have chosen a more stringent category, such as Ocelots with both wizard hats and scarves. Alternatively, she could choose a more lenient category, such as the floor Ocelot category, which can be created with any Ocelot. More complex categories are possible, such as a category of Mortys that can be minted with one Ocelot or two armadillos (NFTs from completely different projects).

In this case, she chooses to mint Wizard Hat Ocelot Mortys because they have the best combination of price and existing liquidity on Uniswap.

Selling Mortys

Alice sells her 50 Mortys on the Uniswap Wizard Hat Ocelot Morty / ETH market, reducing her Vault balance to 50 Mortys.

Purchase Pool

From the buyer's perspective (in this case, Uniswap LP), these Mortys have no connection to Alice's specific Vault. Instead, each Morty represents a share of ownership in the Wizard Hat Ocelot purchase pool, collectively forming the counterparty for Alice and all other Wizard Hat Ocelot Vault owners.

Martingale Settlement

Now that Alice's Vault balance is no longer 100, the Martingale Settlement process begins.

Every night at midnight, the Morty protocol flips a coin for each Vault. If the coin lands heads, Alice sends one of her Mortys to the purchase pool. If it lands tails, the purchase pool gives one Morty to Alice.

So, after the first flip, either Alice has 51 Mortys and the purchase pool has 49, or Alice has 49 Mortys and the purchase pool has 51.

This process repeats daily until Alice has 0 Mortys or 100 Mortys. If she has 0 Mortys, she will hand over all the Ocelots currently in her Vault to the purchase pool. If she has 100 Mortys, she will reclaim her Ocelot. Either way, the process will end.

Martingale Math

Because each coin flip is fair, this process is called a Martingale, meaning Alice's expected Morty balance never changes.

This means that if Alice has n Mortys on a given day and does nothing, she has an n% chance of reclaiming her Ocelot (see proof here). In other words, by selling 50 Mortys to the purchase pool, Alice has effectively sold 50% of her Ocelot.

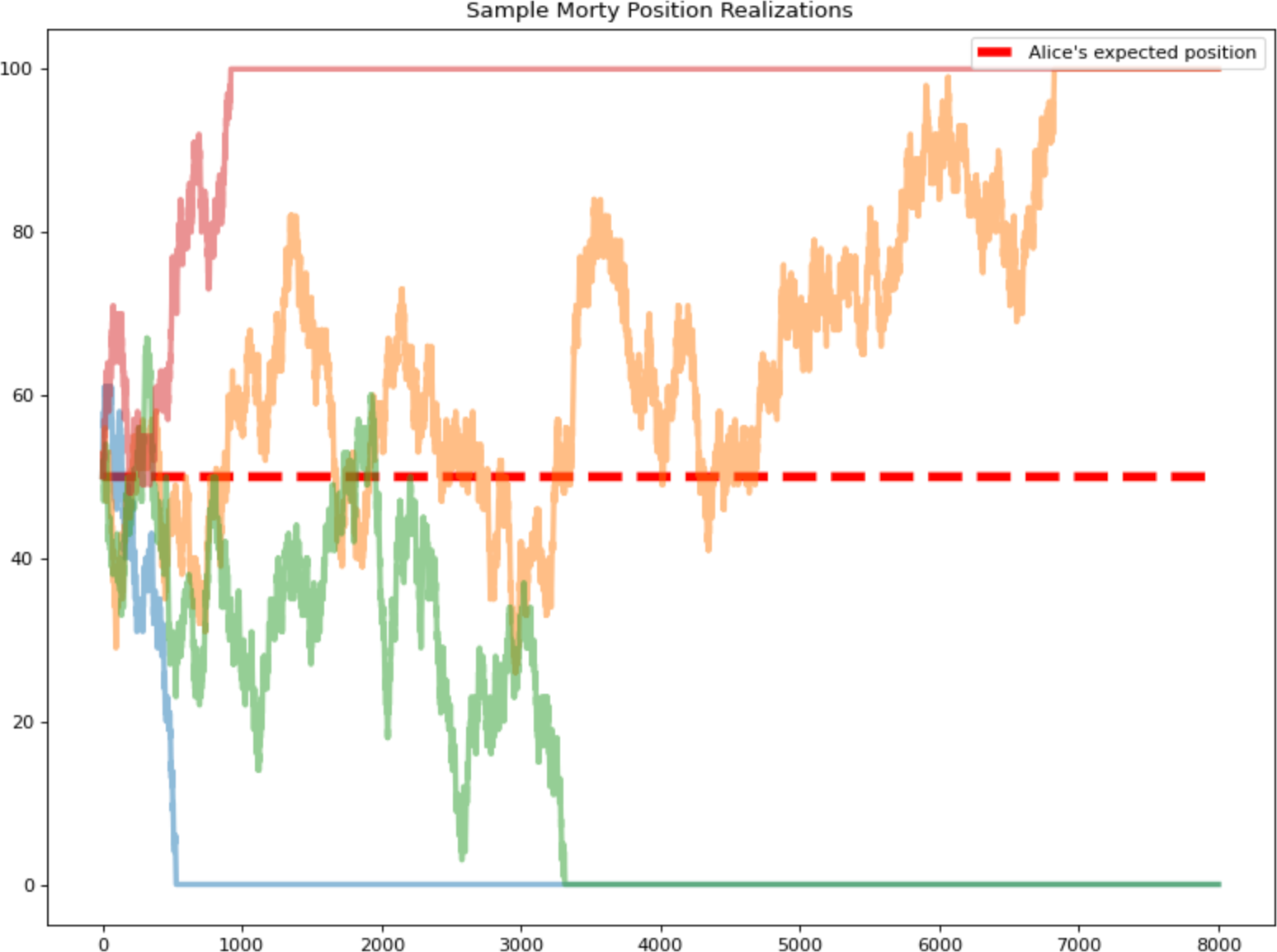
View: ++https://colab.research.google.com/drive/1tMq0Cqa5o3T-da9m0WdBqou2CJ7QMChQ?usp=sharing++

Seller NFT Recovery

If luck is not on her side, Alice has two different ways to reclaim her Ocelot.

The first method is to replace the Ocelot in her Vault with another Ocelot she values less.

The second method is to mint new Wizard Hat Ocelot Mortys or purchase them on the open market and use them to increase her Vault balance, potentially back to 100.

Purchase Pool Settlement

If the Vault balance reaches 0, ownership of any Ocelots inside it will revert to the purchase pool, at which point there can be many different design choices.

For example, the Ocelots could enter an NFTX-like Vault, where anyone can redeem them at the cost of 100 Mortys, plus fees for incentivizing pool liquidity. From this perspective, Mortys can be seen as a potential extension to protocols like NFTX.

Incentives

Vault Owner Incentives

When Alice chooses to mint and sell Mortys using her Ocelot, she risks losing it. Why would she do this?

First, assume there is an active market where she can quickly gain liquidity at a fair price.

Second, there may be significant long-term demand for NFT categories like wizard hat Ocelots, especially from those who cannot afford to buy an entire wizard hat Ocelot themselves. Because Alice is meeting this demand and taking on the risk of doing so, she may be compensated in a way that is higher than what she could obtain by directly selling her Ocelot.

Third, while Alice currently faces Martingale risk, she has eliminated a significant portion of the floor price risk for wizard hat Ocelots. Depending on the price fluctuations of Ocelots, her overall risk may be significantly reduced.

Vault Incentives

The existence of a liquid Morty market could be very beneficial for the ecosystem of its parent NFTs. For example, Morty prices could serve as an index for insiders.

Given the important role of Vault owners, it may make sense to incentivize them directly. For instance, the floor perp protocol could allocate part of its profits to compensate Morty Vault owners who provide their shares for LP in the Morty market on Uniswap.

Malicious Recovery

The purpose of Martingale Settlement is to ensure that Morty buyers have a probability of claiming the NFT. However, there is a potential attack vector that could prevent this from happening.

If Alice opens 50 different Vaults, on average, she will lose 25 Mortys and gain 25 Mortys with each flip. By moving these Mortys between her Vaults, she can stabilize their balances over time.

If this behavior becomes widespread and negatively impacts the perceived value or utility of Mortys, the Morty protocol could charge Vault owners fees when they add Mortys to their Vaults and forward the income to the purchase pool.

A simpler solution would be to disable the ability to add Mortys back to the Vault, as the ability to swap collateral still allows Vault owners to save the NFTs they do not want to lose.

Purchase Pool Risks

Alice's risks in this system are relatively easy to understand: if her Vault balance is 50 Mortys and she does nothing, she has a 50/50 chance of losing her Ocelot. The buyer's situation is a bit more complex.

Basic Case

First, assume Alice is the only Vault owner in the system, and she has sold 10 Mortys, with 5 sold to Bob and 5 sold to Charlie. If Alice wins her first coin flip and gains 1 Morty, then Bob and Charlie will collectively lose 1 Morty, or 0.5 Morty each --- a full 10% of their position.

More Vaults

However, as more Vaults are added, the relative risk for Bob and Charlie begins to diminish. Suppose there are n Vaults, each shorting an average of 50 shares, so the purchase pool includes 50n Mortys.

The number of flips won by the purchase pool forms a binomial distribution with variance n/4.

Bob and Charlie still each own 10 shares, or 1/(5n) of the total, and their variance will be 1/(20n) per flip, quickly shrinking as n increases.

Automatic Cancellation of Flips

If there are at least two Vaults, we can completely eliminate long variance.

Imagine there are an even number of Vaults, say 4. In this case, we can randomly pair them, and each pair only flips a coin once, so the "heads" flip of the first member in a pair will automatically become the "tails" flip of the second member. Note that while we are reducing the degrees of randomness in the system, each individual Vault will still experience Martingale.

Thus, even though the balance of a single Vault will change with flips, the number of outstanding long Mortys will never change. Even with an odd number of short Vaults, we can use this method by randomly selecting one Vault to exclude from the current round of flips.

Alternative Martingales

We can also change the random process used for settlement, as long as it remains a Martingale.

For example, the aforementioned coin flip process may take a long time to complete. What if we designed a process that guarantees completion within a fixed time?

Suppose Alice's Vault is short n Mortys within a designated time frame (meaning its balance is 100-n).

Our alternative Martingale system randomly decides whether to return all n Mortys or let her leave with her NFT, or increase her short position by one Morty. To be a Martingale, she must have a 1/(n+1) probability of reclaiming n Mortys and a n/(n+1) probability of shorting an additional Morty.

For example, if Alice has just minted and sold 2 Mortys, her balance would be 98 Mortys, and she would have a 1/3 chance of getting 2 Mortys back, reaching a total balance of 100, and a 2/3 chance of losing one Morty, resulting in a balance of 97. Her expected return is 1/32 - 2/31 = 0.

This is the necessary process to become a Martingale.

At each time step, Alice either closes her short position and reclaims her NFT or increases her short position by one Morty. Unless she buys or mints more Mortys and adds them to her Vault, the process will always end in 100 time steps.

View: ++https://colab.research.google.com/drive/1tMq0Cqa5o3T-da9m0WdBqou2CJ7QMChQ?usp=sharing++

Conclusion

Mortys are a strange but mathematically pure way to create fractional exposure to an NFT category.

It is still unclear how much market demand there will be for them, but they are certainly interesting to think about.

If they inspire your imagination, I would love to hear your thoughts. You can email me at dave@paradigm.xyz or reach out on Twitter @Dave__White‌.
Source link: https://www.8btc.com/article/6686444