A lengthy article: Systematic Thinking on the Web3 Financial Underlying Framework from the Perspective of Financial Circuit Theory

2022-10-04 18:30:03

Collection

The Web3 financial system needs to be supported by a more systematic structure and actual value for new development, and financial engineering will play an important role in bridging technology and market demand.

Scan with WeChat

*Written by: Gary Yang, Founder of Starry Sky Capital, *"Principles of Financial Circuits and Web3 Economic Models"

After Token2049, the Web3 market has become more determined to quickly break through bottlenecks to seize the next explosion point. With the countdown to the transition between bear and bull markets, leading the next paradigm by seizing the opportunity is certainly the expectation of all Web3 participants. However, the noise is loud but the impact is small; the excitement in the bear market cannot resolve the issues of investor confidence and the bottlenecks in entrepreneurial models. When discussing tokenomics and selling pressure, whether from traditional finance or gaming expertise, or the ponzinomics logic commonly used by Web3 projects over the past year, it is not easy for GameFi or SocialFi projects to make the deal. Everyone realizes that the Web3 financial system needs to be supported by a more systematic structure and actual value for new development, thus the concepts of financial engineering and real yield have emerged, gradually attempting to build new consensus expectations.

The reason Web3 is a value network stems from the combination of blockchain and cryptographic algorithms, making it possible to empower networks and information systems through protocols to achieve "code is law," fundamentally improving commercial contract tools, enhancing the efficiency of financial transactions and the fulfillment capabilities of businesses, thereby improving the overall operation and production efficiency of society.

The infrastructure construction of Web3 is still in its early stages. Such a vast new system inevitably comes with numerous opportunities for change at the infra layer, protocol layer, product layer, and application service layer. Financial engineering will play an important role in bridging technology and market demand. It is not difficult to find that the designers of Web3 financial systems and economic models are very similar to traditional financial macroeconomic policymakers; both need to use systematic engineering thinking to modularize social supply and demand, operational circulation, management mechanisms, and professional services, thereby forming a system engineering. Although there are relatively mature financial engineering concepts in traditional finance, the social environment of textual laws and human handling has many non-standard issues in basic affairs, which still cannot push social efficiency to the next civilized era.

The smart contracts of the Web3 value network stand on the shoulders of the development of the internet to solve this problem. Protocols and contracts can standardly package financial behaviors, transaction behaviors, business needs, and economic strategies using code, allowing financial systems and economic models to enter the era of digital modularization. Coupled with the internet connecting these components, forming a loop, financial engineering transforms and upgrades into financial circuits.

Last year, I first began to think about the concepts of financial circuits and financial chips. Building a financial system is akin to constructing a circuit, viewing cash flow as electric current, value differentials (which will be explained in detail later) as battery voltage, and cash consumption as resistance. A simple financial circuit is thus completed, which seems very straightforward. But first, how do we represent the relationships among these components? Do tools like wallets, aggregators, and staking have clear meanings in the financial circuit? Moreover, how many other advanced financial components are there, and what are their commercial significance and interactions? These require further in-depth thought, which will be elaborated on later in this article. In fact, the evolution of financial circuits will be very systematic. As the ecosystems of GameFi and the Metaverse continue to take shape, the complexity and professionalism of economic model designers will rapidly increase as they incorporate various modules into financial circuits, fundamentally changing our understanding of traditional finance. Eventually, we may witness the phenomenon of emergence (Note 1), potentially leading to applications similar to financial AI and financial chips in the future.

The emergence of financial circuits will undoubtedly greatly enhance the efficiency of market finance and economic commerce, and will evolve into more new-generation capabilities that traditional finance cannot achieve, just as the development of traditional electrical circuits from the 19th to the 20th century led to chips and AI. The future of financial engineering and the financial circuit industry will achieve complete innovation, bringing social and economic efficiency to an astonishing state; from a financial perspective, just as the earliest financial derivatives emerged in the 14th century and evolved into a global financial trading system in the 20th century, the meaning of finance itself will further evolve into a more advanced complex system with the development of technology.

It is worth mentioning that the emergence of NFTs has actually become an important tool for the feasible development of financial circuits. Although NFTs have mostly appeared as small image assets since their market debut with Cryptokitties in 2017 to today's Opensea and LooksRare, their significance is profound. NFTs are essentially containers; from a technical and coding perspective, they are digital containers of metadata, and from a commercial finance perspective, they are value containers. Under the definition of protocols, NFTs are important tools for realizing the feasibility of financial value packaging. In this regard, cutting-edge Web3 projects like Solv Protocol have already built a relatively complete system framework from the protocol layer to the product application layer, combining protocols, smart contracts, and splitable NFTs to provide more advanced product services and more effective financial engineering components for the next stage of the financial market.

For designers of Web3 financial models and economic models, they constantly face events involving cash flow management, liquidity unlocking, buying pressure, burning, staking, and other issues in their work. These are the most common operations encountered in market project management. Frequently, designers will create financial flow diagrams, incorporating various modules, such as deflationary and inflationary dual-token models, staking schemes, liquidity pools, bonus pools, and VE mechanisms, among others. For every Web3 economic model designer, PM, and technical engineer, they are already dealing with specific issues of financial circuits with varying degrees of complexity. Currently, some in the market have proposed the concept of financial Lego; however, I believe this is not suitable for constructing the underlying framework of Web3 finance. The Lego model is essentially a stacking of non-standardized business modules, not a structured theory that can be applied to future commercial management of projects. The development of financial circuits requires a complete foundational theoretical system for support, while upper-level applications can certainly be tailored to individual needs.

So, will financial circuits possess systematic theoretical characteristics similar to physical circuits? For instance, can we simply say there is a relationship between voltage and current akin to Ohm's Law, or delve deeper into classic theories like Thevenin's theorem (Note 2) and Kirchhoff's laws (Notes 3, 4) in circuit principles? Can financial circuits under economics similarly have such model principles? The answer is affirmative. It can be stated that not only are they similar, but there is a complete paradigm correspondence, and this paradigm correspondence system will have significant implications for the future development of financial circuits. The following content will discuss several aspects:

The significance and explanation of financial circuit elements -- What common elements and components are there in financial circuits?
The principles and significance of financial circuits -- The theorem significance of financial circuits and the relationships among various elements and components.
The significance of economic models and discussions of classic problems -- How to use financial circuits as a method to think about Web3 issues.
The paradigm differences between financial circuits and physical circuits -- Viewing financial circuit issues from the perspective of social practice science.

The significance and explanation of financial circuit elements

The flow of cash in finance is very similar to the flow of electrons in a circuit; this is essentially the source of the financial circuit. In an electron flow, electrons flow, while in cash flow, cash flows. This correspondence only requires a clear definition of cash amounts and cash flows to connect with circuit principles. A relatively abstract question is: what exactly is voltage? This is a crucial economic concept discussed in this article, namely value potential difference, which is essentially the essence of value. What we repeatedly say about escaping ponzinomics to find real yield is essentially about discovering the process of real value generation and the essence of value. In economic and financial circuits, value needs to be defined as an objective potential field, just like an electric potential field, so that the issue of voltage can be resolved.

Next, we will accurately define the most basic elements and components of financial circuits. This is the first step in forming a complete system and a prerequisite for corresponding with physical circuit principles. In defining elements and components, I have tried to choose names and symbols that are the same or similar to those in physical circuits to maintain correspondence.

1. The most important basic elements of financial circuits:

Quantity of cash (q), referred to as cash

The quantity of cash is the most important basic element of financial circuits. It is simply the amount of money and the number of tokens held.

Cash flow (i), referred to as cash flow

Cash flow is familiar to anyone who has studied finance in a company, but what exactly is it? Simply put, it is the cash that passes through your hands over a period of time. This is analogous to the relationship between current and charge, defined as i=q/t. The size of cash flow is essentially a measure of intensity, indicating the capital flux per unit time. Additionally, the direction of cash flow simply refers to the direction of cash movement, which is different from physical circuits (Note 5), but is more intuitive and easier to understand.

Value potential difference (v), referred to as value

Value is the basis of financial exchange. Only with a value potential difference will cash flow occur; with information asymmetry and value asymmetry, cash will flow from value lowlands to value highlands, which is the process of cash pursuing value exchange. Conversely, cash at a high value position will not choose to flow and exchange towards a low value position when information is sufficient, as there is no value potential difference to supply cash for exchange. Here, I would like to add a concept of value potential, which, although somewhat abstract, is quite simple. It expresses an objective height of value; there exists a value potential difference between two entities at different value potentials, indicating the presence of business opportunities, investment opportunities, or trading opportunities. It is important to note that in actual financial business environments, information is often asymmetric. Sometimes cash may mistakenly believe it is at a high value position due to FOMO emotions, misjudgments, or phishing scams, leading to price bias. From a micro perspective, price bias is essentially cash being at a value position it should not be in, and ultimately, due to information release or unmet expectations, it cannot sustain (stay at that position). At this point, cash will quickly pour down from an unreasonable position, forming selling pressure, which is also the process of price returning to value. The financial circuit in the actual market is socialized, differing from the classic physical model of electronic circuits, and will often exhibit various cash value misalignments due to information asymmetry and value asymmetry, frequently causing cash q to appear at inflated value positions, or even falsely inflated positions. In many cases, the selling pressure risks in the financial environment are significant, though under non-extreme conditions, they are also healthy, as only through circulation can economic finance and value exchange occur. The value potential difference can be said to be a very important concept in financial circuits; without a value potential difference, a system can only construct short-term misaligned value potential differences internally, engaging in zero-sum games based on information asymmetry, lacking sustainable development significance. This is also the current market concern of investors regarding the continuous internal competition of GameFi and SocialFi projects within the logic of ponzinomics.

Resistance of burning (r), referred to as resistance

Resistance of burning encompasses many forms. From a basic perspective, because supporting blockchain operations requires paying gas fees to miners, resistance is inherently present in the Web3 financial system. Additionally, in different protocols and applications, platforms and project parties can customize consumption, loss, and destruction mechanisms, all of which are characteristics of resistance. In the operation of an economic system, both macro managers and micro project parties need to implement certain consumption mechanisms to control inflation within the financial system, which is very important. Simultaneously, from the user's perspective, completing specific tasks also requires certain expenditures, which is quite normal. This process of system consumption from macro to micro is a very important foundational task in the design of financial circuits and economic models, thus the design of resistance is quite skillful. However, the concept of resistance is not easy for users and the general public to understand and use directly. For users and the general public, what they are more concerned about is actually the quantity of cash/tokens burned by resistance, referred to as cash/tokens burned. The consumption amount is essentially the amount of cash consumed under resistance r over a certain period through cash flow (this will be specifically mentioned later in the financial Thevenin theorem). What users care about is how much fee they paid and how much value they lost during the process of completing a task to obtain value or services. In fact, designers of economic models and financial systems will adopt many liquidity management methods, functions, and tasks to create resistance in the process of suppressing inflation. These methods are called deflation mechanisms, aimed at continuously consuming cash within the system and maintaining the operational balance of economic models and financial systems.

2. Important components in financial circuits:

Source of real yield (y), referred to as yield

A term that has been increasingly mentioned in the Web3 market is real yield, which advocates that Web3 must escape the bubble issues of blockchain and crypto in previous cycles. The value proposition of projects must have actual economic and commercial significance, and project teams must seriously deliver project value, whether deciding to generate liquidity on day one or choosing to build a team in a Web2 style to attract traffic. The behavior of projects obtaining financing from the market or issuing tokens is essentially a process of generating value potential difference expectations from the yield source after establishing a narrative logic of value proposition, thus generating or attracting cash flow (Note 6).

The yield source is a relatively special financial component because it generates value, creates potential differences, and is the reason for the initial flow of cash. In physical circuits, it corresponds to battery voltage or voltage sources. Financial components outside the yield source can generally be divided into linear financial elements and non-linear financial elements, with the former being common and simple financial components that have been widely applied in current Web3 market project designs, including the following three forms:

Resistance elements (r), already introduced in the basic elements;
Capacity elements of cash/tokens (c), referred to as capacity

This is relatively easy to understand. In actual financial circuits, the most common container elements are wallets and their aggregators, where a wallet can be an address opened by a DEX or an account provided by a CEX (centralized platform) that packages a series of addresses. Regardless, these containers provide users with a place and medium to store cash. Once cash enters these containers, users have relatively autonomous control over liquidity; generally, they will not withdraw everything at once or leave it completely idle. For the entire financial system, although there is no micro control over the cash in the containers, it can enjoy the buffering effect generated, dispersing and asynchronizing cash flow, thus alleviating liquidity pressure. This process is very different from the value of staking elements. However, when the financial system where the containers are located encounters significant external factors leading to systemic issues (here, the financial system can refer to a single project or a larger ecosystem), many users may simultaneously make the same or similar decisions, such as withdrawing liquidity or depositing into wallets at the same time. At this point, the entire system may face the risk of a death spiral or the expectation of a flywheel effect.

Staking elements of cash flow/tokens (s), referred to as staking

Staking elements in actual financial circuits manifest as staking mining, liquidity pools, linear prize pools, internal digital assets of economic models, and other cash flow staking schemes that have asset preservation and storage value characteristics. Their characteristics in financial circuits are: when the financial system and cash flow are relatively stable, staking is not necessarily required (of course, most financial systems are unstable without staking). However, when the financial system experiences significant cash flow fluctuations, various staking methods are needed to retain cash in a certain place, balancing system cash flow through time differences. This process usually requires the system party to reward participants in staking with certain costs. The main difference from resistance is that this process does not consume cash; instead, after a period, when cash is returned, a certain reward must be supplemented (some may ask why not just use resistance; the reason is that users are unwilling, and the system needs to incentivize users to retain them, protecting the overall cash amount and liquidity stability). The main difference from containers is that users do not have strong control over staked cash; rather, they receive corresponding contractual returns after a certain period through a contractual form, while the platform or system can exchange certain costs for management dominance over part of the cash flow for a period, balancing time differences across various loops in the financial circuit, ensuring that the system does not experience cash flow droughts or cash flow bottlenecks.

In addition to the three most important components (collectively referred to as) financial circuit impedance elements (represented by z), more complex non-linear financial elements will inevitably emerge during the development of financial circuits, similar to PN junctions in physical electronic circuits that gradually evolve into diodes and transistors, ultimately evolving into various more complex financial chips and financial components. Here, I will not expand on this imagination. In fact, some financial projects have already applied non-linear financial elements through random prize pools, blind boxes, or random airdrops using random functions and non-linear functions, but these are still very rudimentary applications, and there is vast room for development.

The principles and significance of financial circuits, comparing financial circuits with physical circuits

Based on the definitions of the basic elements and important components of financial circuits mentioned earlier, it is not difficult to see that financial circuits and physical circuits share paradigm characteristics in all basic properties, thus it is entirely possible to derive a complete set of financial circuit principles based on the foundational principles of physical circuits, which is undoubtedly good news for the construction of Web3 financial systems.

The relationships among various elements and components of financial circuits conform to the basic laws of financial circuit principles derived from the physical circuit paradigm. The following sections will select some basic principles and laws for explanation, and I will attempt to describe their general expressions, financial significance, practical characteristics, special situations, and extended meanings as intuitively as possible.

First, let’s revisit the issue of cash flow. In the principles of financial circuits, cash flow is the amount of cash passing through a certain node per unit time, i.e., i = q / t. This is the most basic element of financial circuits. Cash flow is akin to electric current, water flow, or blood flow; managing cash flow is comparable to circuit design, urban water management systems, or the process of blood delivering nutrients throughout the body. It is both the carrier of economic circulation and the core driving force behind the operation of financial circuits.

Next, let’s look at the laws and properties of the three basic financial components, specifically how financial consumption resistance, container elements, and staking elements work under a certain value yield source:

Financial resistance Ohm's Law, properties of financial container elements, properties of financial staking elements

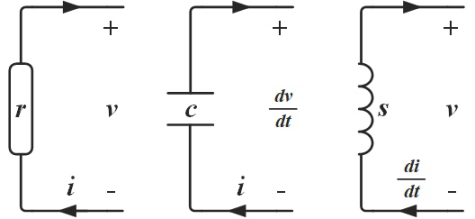
Financial resistance Ohm's Law:

General expression: i = v / r (cash flow = value / resistance)

Financial significance: In the presence of a value potential difference, cash flow is inversely proportional to consumption resistance.

Practical characteristics: If there is value in the market, users and investors will show interest in it, reflected in their desire to invest in its value or continuously spend money to purchase its products. If the project or platform sets a high resistance, such as high transaction fees or many additional costs, it will dampen the enthusiasm of investors or buyers, reducing cash flow; conversely, the opposite is true.

Special situation: When resistance is infinitely large, cash flow is zero; in extreme consumption resistance scenarios, even if there is value, there will be no cash flow to use this product. Additionally, when the value difference is zero, cash flow is also zero; if the product itself has no value, even without resistance, there will be no cash flow to buy this product.

Extended significance 1: Based on i = q / t, we can derive qr = vt / r, indicating that under certain value potential differences and resistances, the cash consumed by users when using a valuable product qr is proportional to time.

Extended significance 2: Series and parallel resistance; series resistance represents adding two resistance methods to increase the consumption of cash flow by users; parallel resistance in financial circuits is quite special; unless the project party states that both task lines must be completed to obtain value, this situation is similar to the meaning of parallel resistors in traditional circuits. Typically, the result of parallel financial resistance will cause users to choose only one path to obtain value, abandoning the other path, resulting in that line being disconnected with no cash flow; this needs to be defined by the project party; disconnection is akin to adding a switch in the circuit, not due to mismatched paradigms of parallelism.

Properties of financial container elements:

General expression: i = c · dv / dt (cash flow = container parameter * rate of value change)

Financial significance: When value changes, cash in the container elements will flow in or out.

Practical characteristics: Only when external value changes do people consider taking cash out of their wallets or depositing cash into them, forming cash flow; if external value remains unchanged, meaning there are no investment or consumption opportunities, the cash amount in the container elements does not change, and no cash flow is generated.

Special situation: When value does not change, i.e., dv/dt = 0, regardless of how much cash is in the container elements, cash flow will be zero; if the container elements cannot hold cash, i.e., c = 0, regardless of how value changes, there will be no cash flow passing through because there are no wallets or other container carriers.

Extended significance: c = ∫ i dt / v, when value is discovered, cash will continuously flow out of the container elements, and after a certain period, the total amount of cash flowing out equals the carrying capacity of the container elements (specifically, the product of carrying capacity and value, depending on the definition of carrying capacity dimensions in different economic models).

Properties of financial staking elements:

General expression: v = s · di / dt (value = staking parameter * rate of cash flow change)

Financial significance: When cash flow changes, staking elements will carry independent value.

Practical characteristics: The concept of staking is essentially value residing. From the user's perspective, whether storing cash in a liquidity pool to earn interest or investing in a certain NFT asset to complete tasks, it is essentially a concept of cash flow locking for a period, fundamentally reflecting the user's recognition of partial value over a specific time. From the macro perspective of project parties and model managers, if cash flow does not fluctuate due to users' buying and selling decisions, it indicates that value is held by the project party itself, and there is no need to establish staking modules to balance cash flow. However, typically, once cash or tokens are distributed to a certain proportion, project parties and model managers can no longer fully control the value of the project and model. A large number of buying and selling transactions will occur in a marketplace, necessitating the use of staking to periodically indirectly recapture some liquidity to reduce pressure on system management. In fact, similar properties exist in macroeconomics, such as government bonds, pensions, and reverse repos.

When cash flow changes rate is zero, the staking function has no value, and the staking value is zero; if cash flow changes very dramatically, the value of staking in the system will also be expected to be very large, but in real environments, there will be emotional thresholds or system entropy increases, which is essentially a singularity problem. At this point, staking may become ineffective or lead to a liquidity trap (Note 7).

Extended significance: s = ∫ v dt / i, after cash flow fluctuations activate the staking elements, the total value of staking over a certain period equals the product of the staking capacity of the staking elements and the cash flow passing through them (this depends on the definition of staking capacity dimensions in different economic models).

In actual Web3 economic financial environments or in the design of some project economic models, most situations involve designers arranging and combining the aforementioned three basic financial elements, managing cash flow in economic models through their series and parallel properties.

One point not discussed above is the financial significance of the yield source. In fact, when project parties consider single-token models, dual-token models, or whether to introduce a new NFT digital asset (Note 8), they are essentially increasing the yield sources in the financial circuit. Different yield sources act like battery packs, serving different roles; for example, the coordination of deflation and inflation is a good example.

It is worth noting that many yield sources are not activated or lit at the beginning; as the project develops, they gradually become liquidity sources through attracting financing, such as financing, listing, and liquidity pools.

With the support of these model structures, we can draw the structure of financial circuits. In Web3, from a business perspective, we can refer to it as the tokenomics network. Let’s look at a practical example; the following diagram is a simplified representation of a real project case in the Web3 market. The actual economic model will have various micro-adjustments in local parts, but here only the main structural line is presented for reference:

Due to the complexity of actual projects, this model structure already contains non-linear elements. Among them, y2 is a non-linear adjustable yield source, while r1, r2, r3, rm1, and rm2 are all non-linear adjustable consumption resistances. In actual situations, project parties and managers often do not disclose all functions and structures, especially since many consumption resistance parts have hidden conditions. Typically, linear elements and linear parameters generally represent major or simple rules, while non-linear parts are selectively disclosed by designers and managers, or will soon be reverse-engineered by users or research parties in the OTC market through numerical methods.

Aside from the basic principles mentioned above, deeper theorems and laws from physical circuit principles are also applicable in financial circuits. Below, I will use Thevenin's theorem and Kirchhoff's laws as examples to correspond their paradigms to the foundational theorems in financial circuits:

Financial Thevenin's Theorem

Theorem description: A linear economic model network containing independent yield sources and linear financial impedance elements can be equivalently represented by an independent yield source v and a series financial impedance element z.

Financial significance: Similar to the Thevenin's theorem in circuit principles, the financial Thevenin's theorem is a method for simplifying the analysis of economic model networks, used to convert complex financial circuits and economic model networks into simple equivalent networks, facilitating project comparison analysis and investment analysis.

Financial Kirchhoff's Laws

Theorem description: Financial Kirchhoff's cash flow law: The total cash flow entering a node equals the total cash flow leaving that node; that is, if the sum of cash flow entering a node is positive and the sum of cash flow leaving that node is negative, then the algebraic sum of all cash flows involving that node equals zero. The formula is expressed as: Σ ik = 0 (k=1,2,…,n).

· Financial Kirchhoff's value potential difference sum law: In a closed financial circuit loop, the algebraic sum of the value potential differences across all financial elements equals zero; that is, the algebraic sum of all value potentials along the closed financial circuit loop equals the algebraic sum of all value potential differences. The formula is expressed as: Σ vk = 0 (k=1,2,…,n).

Financial significance: The reasoning is quite simple. For the cash flow law: Any node, like a wallet address, has equal total cash flow in and out, treating inflows as positive and outflows as negative, with their total conserved at zero (some may ask, does issuing tokens or NFTs by the project party break this rule? No, these are not nodes but rather yield sources). For the value potential difference sum law: In a closed economic model system, during the internal circulation of cash flow, the total value potential difference traversed equals zero, meaning either all value potential differences will eventually be leveled out, or there will always be information asymmetry and value asymmetry, causing high and low value positions to correspond equally, indicating that there are usually people who misjudge their value positions.

In addition to Thevenin's theorem and Kirchhoff's laws, many other theorems in physical circuits, such as Norton's theorem, can also be paradigm-transformed into corresponding theorems in financial circuits, which I will not elaborate on here.

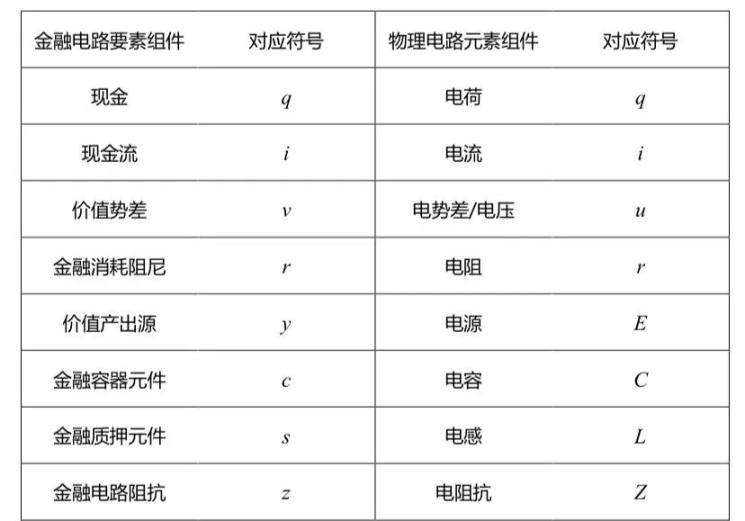
Finally, I will provide a comparison table of parameters between financial circuits and physical circuits for reference:

Comparison table of parameters between financial circuits and physical circuits

The significance of economic models and discussions of classic problems

The financial circuit analysis methods above can serve as effective tools for structuring and analyzing economic models from many aspects, further assisting Web3 projects in designing and managing solutions through engineering and digital quantification. From micro to macro, models can be generalized to conduct data research on market environments; conversely, they can also be reverse-engineered to quantify analyses of local structures in finance and commerce.

Based on the financial circuit concept, as illustrated in the real project case discussed in the previous section, we can clearly express project economic models using the tokenomics network diagram, facilitating management synchronization, project communication, task division, and adjustments. Additionally, over a certain time scale, the economic model network simulated by financial circuits can serve as a foundation for numerical simulation of financial circuits, numerical calculation of financial circuits, and sandbox simulation of tokenomics, allowing for predictions of market finance, commercial value, and the direction of the digital economy.

In various projects I have encountered over the past few years, many have faced issues at the starting point of economic model design due to a lack of a systematic approach from day one. Consequently, they may not see the overall situation during development due to the absence of a roadmap, only making emergency adjustments in various local areas, making it difficult to achieve overall balance. Furthermore, some projects may become popular due to certain individual application functions being highly advanced, but due to relatively poor overall completeness, they struggle to maintain their leading advantage. As they progress into the mid to late stages, numerous issues and loopholes in their economic models emerge, ultimately leading to an inability to remedy the situation and losing their competitive edge.

I believe such phenomena are about to end as the early development stage of Web3 concludes. As the tools for economic model simulation improve alongside the development of Web3 financial engineering, the entire market will certainly usher in a new stage of development. Financial circuits and economic model networks themselves also represent a way of thinking, capable of explaining many issues related to value positioning, business models, and market phenomena. We can engage in Q&A discussions on some simple questions here:

Q1: How is selling pressure formed?

A1: This is a classic question, and I have already provided some explanation when defining value potential differences. Selling pressure typically arises from information asymmetry or sudden events leading to value misalignment, resulting in price bias, meaning cash is in a value position it should not be in. Cash holders originally believe they are at a high value position, but when information is released, sudden events occur, or overall expectations cannot be sustained, they suddenly realize the problem. Thus, they hope to quickly transport cash to reasonable value positions, leading to a cash outpouring process, which is selling pressure. Selling pressure itself is also the process of price returning to value.

Q2: Will some projects add invisible consumption in their economic model design?

A2: Yes. In addition to gas fees, project-defined transaction fees, and various declared consumption scenarios, many economic models actually have many invisible resistances behind them, some of which are very hidden. Particularly in some non-linear financial elements, seemingly simple business models often hide adjustable resistances in many details, which have already been widely applied in traditional finance and commerce.

Q3: Will AMMs repeat the mistakes of Luna/UST, and is there an effective way to resolve the imbalance of UST's AMM?

A3: I believe some will. In the protocol, defining non-linear increasing resistance after trading volume exceeds a certain threshold or price bias reaches a certain level (e.g., 0.5%) can help.

Q4: Can we set special hysteresis resistance in the protocol to prevent issues when selling pressure causes severe price slippage?

A4: This question is a derivative of the previous Q3, which I proposed during a panel discussion. I believe it is possible. This may be a future financial mechanism, similar to a slow-released circuit breaker.

Q5: Can financial circuits and economic model networks explain what Web3 can achieve that traditional finance and Web2 cannot?

A5: I believe many things. The wave of SOS from OpenDAO actually saw Opensea evaluate and decide not to issue tokens, thus supplementing a value yield source in the economic model network. Similarly, projects like People, which capture value from the traditional world, and Klima DAO, which captures value from blind spots in classical macroeconomic theory (Note 9), also follow this principle.

Q6: Is providing staking product functions a short-term solution?

A6: No. Just as inductance is important in circuits, staking methods in financial systems are a crucial link in utilizing cash flow time differences to solve system circulation stability.

Q7: Many Web3 projects have realized that issuing linear rewards through POW will accelerate their entry into a death spiral within ponzinomics. How can this issue be better controlled for liquidity?

A7: First, any economic model without real yield is driven by ponzinomics and will ultimately face a death spiral issue. So, before a project truly finds real yield, can it better control liquidity? In fact, slight modifications to the linear reward model of POW can alleviate many issues. Currently, many projects have abandoned linear incentives in favor of incentivizing users with a fixed total amount daily or weekly, effectively enclosing non-linear yield sources within a segment, ensuring controllable total releases externally.

Q8: Can a single utility token model resist inflation?

A8: This question is essentially a derivative of Q7. Similarly, without real yield, these are merely empty discussions. Also, moving away from linear POW incentive schemes can delay the onset of inflation.

Q9: What do bonds, options, and financial derivatives represent in financial circuits?

A9: For simple financial derivatives, many belong to staking elements or combinations of staking elements, such as bonds. Futures, options, warrants, and put warrants, in my view, are combinations of staking elements and switches. Financial derivatives will be more complex, involving non-linear elements, staking elements, container elements, and switches. Of course, how to define the execution rights of switches, and whether execution rights, credit, and cash are linked, will not be elaborated on here. Feedback is welcome.

( Of course, we can raise many more questions, and all kinds of inquiries are welcome. )

Additionally, based on financial circuits and economic model networks, the market for financial electronic components may develop rapidly. The flexibility of Web3 financial derivatives is vast, and the market space it brings is also significant. Overall, I believe the next stage of financial derivatives will fall into three categories: one part will be existing financial tools and products from traditional finance, which will directly correspond, such as bonds and options mentioned in Q9, rapidly expanding into usable services through Web3 finance in the coming years; another part will be financial products and derivatives transformed into Web3, quickly generating more complex financial derivatives through combinations of code protocols. I believe this part will have about a ten-year adaptation period, but the prospects are very broad; the third way will completely break away from traditional financial thinking, generating a new generation of Web3 financial derivatives based on financial circuits and economic model networks, such as more flexible splitable financial units, AI financial units, and non-linear intractable financial units.

The paradigm differences between financial circuits and physical circuits

Finally, let’s examine the paradigm differences between financial circuits and physical circuits. In fact, similar to other principles in economics, any ideal model's application to social practice cannot be overly rigid and dogmatic. The main reason is that the people, events, and things in social and economic environments differ from the particles in physical environments, exhibiting characteristics of unit heterogeneity, discreteness, and randomness. Only at a relatively macro level will the characteristics of theoretical models be more reflected.

For instance, how to choose the time scale in financial circuits is a relatively important question. For different economic model networks, managers and designers need to determine time choices based on the scale effects of their respective economies. Similarly, each model does not have the same cash flow volume that forms scale effects, and during numerical simulations and sandbox exercises, considerations should be given to the minimum applicable scale and minimum grid scale (Note 10).

Due to the aforementioned discreteness, randomness, micro-fluctuations, and instability, in the future applications of quantitative simulations of financial circuits and economic model networks, as the market gradually matures, it may be necessary to introduce theories of stochastic mathematics and fuzzy mathematics, and use methods such as pulsating equations for simulation solutions.

Special Notes

Note 1: Emergence

The phenomenon of emergence was mentioned by Max Tegmark in his 2018 book "Life 3.0." Here, I borrow its extended meaning, which refers to when the foundational particles and components are numerous, the overall composition will produce a new phenomenon, representing a process of quantitative change to qualitative change from micro to macro.

Note 2: Thevenin's Theorem

A linear resistive single-port network N containing independent power sources can be equivalently represented as a single-port network consisting of a voltage source and a series resistor. The voltage of the voltage source equals the open-circuit voltage uoc of the single-port network; the resistance R0 is the equivalent resistance of the single-port network N0 when all independent power sources are set to zero.

Note 3: Kirchhoff's Laws

Kirchhoff's laws are the basic rules governing voltage and current in circuits, proposed by German physicist G.R. Kirchhoff in 1845. Kirchhoff's laws include Kirchhoff's current law (KCL) and Kirchhoff's voltage law (KVL). Kirchhoff's laws can be applied to analyze both DC and AC circuits, as well as nonlinear circuits containing electronic components.

Note 4: In complex financial circuits, such as financial chips, non-linear financial elements will emerge, which will be mentioned later when discussing financial components. The financial Thevenin theorem mentioned later in this article cannot handle non-linear financial element issues.

Note 5: The direction of current in physical circuits is the direction of positive electron movement. However, in metallic conductors on Earth, most electrons are negative, so the observed current direction is opposite, meaning the current direction in circuits is opposite to the direction of electron flow.

Note 6: Attracting cash flow and investment is, for Web3 systems, a native source of production just like producing tokens, equivalent to viewing the Web3 system as an independent economy that attracts production funds and resources from the Web2 world or traditional financial markets into the new Web3 world. From a physical perspective, this can be seen as opening a wormhole in a semi-closed system, introducing supplies from other spatial systems, which is its own source.

Note 7: Liquidity trap

A liquidity trap is a hypothesis proposed by Keynes, indicating that when the interest rate level cannot be lowered further over a certain period, the elasticity of money demand becomes infinite, meaning that no matter how much money is increased, it will be hoarded. The corresponding meaning of this paradigm is somewhat abstract; when project parties or managers fail to manage severe liquidity fluctuations, staking and various value assets cannot bear cash, leading liquidity to return to container elements or causing system value depreciation, i.e., inflation.

Note 8: NFT digital assets will be very special in financial circuits; they are a special container that can be either active or inactive. When active, NFTs act as a battery, serving as a yield source in financial circuits; when inactive, NFTs can be container elements or staking elements, with more being staking elements, depending on the project party's specific definitions in the economic model design within the protocol.

Note 9: Traditional macroeconomics points out that in non-market economic sectors such as ESG environmental protection, urban construction, and pensions, due to their public welfare nature, policies need to subsidize these economic systems to enable them to form cycles like other market-oriented economic sectors. I believe this is a point of incompleteness in the traditional market economic theory system, thus referred to as a blind spot.

Note 10: Grid scale is a commonly used concept in numerical calculations for physical model simulations, referring to the size of the spatial scale of the smallest computational unit. Numerical calculations can only simulate environments above the grid scale, while factors below the scale, which exhibit many random or unmeasurable elements, are mathematically ignored as higher-order small quantities. This numerical calculation typically produces errors after a certain time length, which is essentially caused by uncertainty overflow within the scale.