Curveステーブルコイン設計ホワイトペーパー（中英対照版）
Curveステーブルコイン設計ホワイトペーパーの中英参照版であり、いくつかの理解を助ける中国語注釈を追加し、原版のスペルミスも修正しましたので、皆さんの参考学習に供します。著者：Michael Egorov, Curve Finance
編纂：JamesX，iZUMi Research**
概要
このステーブルコインの設計には、いくつかの重要な概念があります：貸出-清算AMMアルゴリズム（LLAMMA）、PegKeeper、金融政策が最も重要です。しかし、主なアイデアはLLAMMAにあります：特別目的のAMMで清算を置き換えることです。
このステーブルコインの設計には、いくつかの重要な概念があります：借貸-清算AMMアルゴリズム（LLAMMA）、PegKeeper（安定保持メカニズム）、金融政策。しかし、主な設計ポイントはLLAMMAにあります：従来の過剰担保貸出の清算プロセスを特別用途のAMMで置き換えることです。
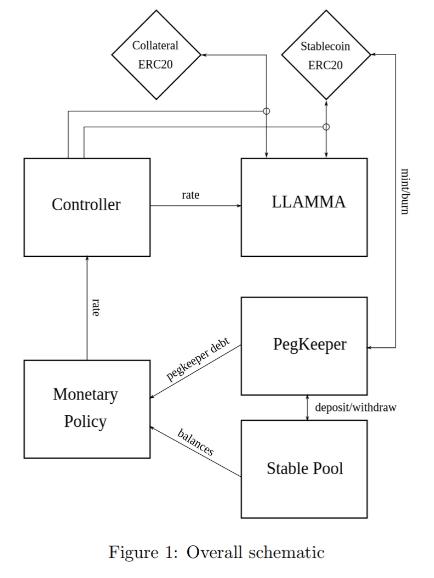
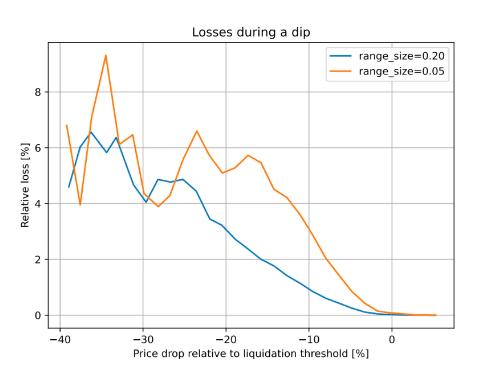
図2：清算閾値に対する価格変動に対する損失の依存性。観察の時間ウィンドウは3日
この設計では、誰かが担保に対して借り入れを行った場合、たとえ清算閾値に達しても、担保の価格が下がって反発しても、重大な損失は発生しません。たとえば、2017年9月以降のETH/USDの歴史的データを使用したシミュレーションによれば、CDPを3日間放置し、その間に価格が清算閾値を10%下回った場合、担保の1%のみが失われます。
この設計では、誰かが担保に対して借り入れを行った場合、たとえ清算閾値に達しても、担保の価格が下がって反発しても、重大な損失は発生しません。たとえば、2017年9月以降のETH/USDの歴史的データを使用したシミュレーションによれば、CDPを3日間放置し、その間に価格が清算価格を10%下回った場合、担保の1%のみが失われます。
継続的清算/非清算のためのAMM（LLAMMA）
継続的清算/非清算のAMM（LLAMMA）
ステーブルコイン設計の核心的なアイデアは、貸出-清算AMMアルゴリズムです。このアイデアは、担保（例えばETH）とステーブルコイン（ここではUSDと呼びます）の間で変換を行うことです。担保の価格が高い場合、ユーザーはすべてETHで預金していますが、価格が下がるとUSDに変換されます。これは、従来のAMM設計とは大きく異なり、従来のAMM設計ではUSDが上にあり、ETHが下に配置されています。
以下の説明は、完全に自己一貫した厳密な証明として機能するものではありません。その多く（特に不変量）は、次元的な考慮から得られています。完全な数学的記述を持つにはさらなる研究が必要かもしれませんが、以下の内容は実践での実装に十分であると考えられています。
これは外部価格オラクルによってのみ可能です。要するに、典型的なAMM（例えば、ボンディングカーブが双曲線の一部であるもの）を作成し、その「中心価格」を（例えば）下から上に移動させると、トークンは（例えば）USDからETHに絶熱的に変換され、途中で両方向の流動性を提供します（図3）。これは、量子物理学における回避交差（ランドー-ゼナー遷移とも呼ばれる）にやや似ています（ただし、アイデアとしてのみ：プロセスの数学的記述は非常に異なる可能性があります）。流動性が集中する範囲はここではバンドと呼ばれ、定常的なpoバンドにはpcdからpcuまでの流動性があります。私たちは、pcd(po)とpcu(po)がpoの関数であり、関数が線形よりも急であり、したがってpoよりも早く成長することを求めています（図4）。さらに、価格p↓とp↑を定義し、p↓(po) = po、p↑(po) = poとし、絶熱的な限界でのバンドの端を定義します（例えば、p = po）。
これは外部オラクルによってのみ実現可能です。要するに、典型的なAMM（例えば、ボンディングカーブが双曲線の一部であるもの）を作成し、その「中心価格」を（例えば）下から上に移動させると、トークンは（例えば）USDからETHに絶熱的に変換され、途中で両方向の流動性を提供します（図3）。これは、量子物理学における回避交差（ランドー-ゼナー遷移とも呼ばれる）にやや似ています（ただし、アイデアとしてのみ：プロセスの数学的記述は非常に異なる可能性があります）。
流動性が集中する範囲はここでは「バンド」と呼ばれ、定常的なpoバンドにはpcdからpcuまでの流動性があります。私たちはpcd(po)とpcu(po)がpoの関数であり、関数が線形よりも急であり、したがってpoよりも早く成長することを求めています（図4）。さらに、価格p↓とp↑を定義し、p↓(po)=poとp↑(po)=poの価格として、絶熱的な限界でのバンドの端を定義します（例えばp=po）。
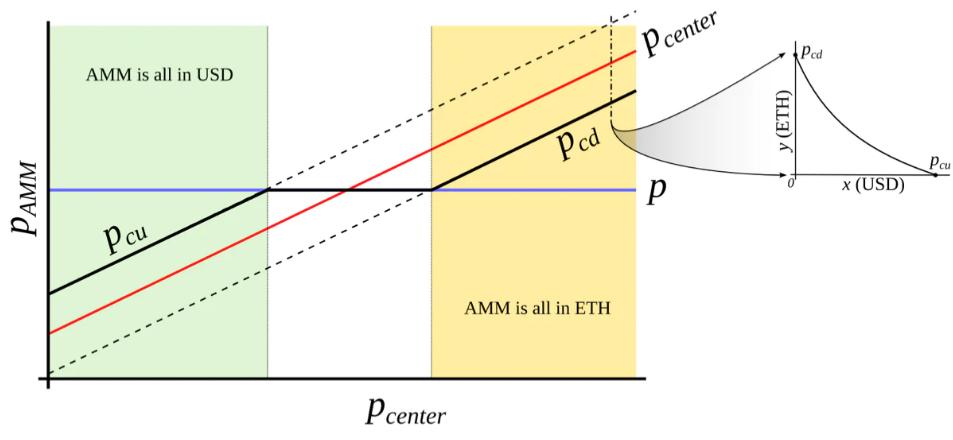図3：「外部価格ソースを持つAMM」の挙動。外部価格pcenterは流動性が形成される価格を決定します。AMMは価格pcdからpcuまでの流動性をサポートし、pcd < pcenter < pcuです。現在の価格pがpcdとpcuの範囲外にあるとき、AMMはpcuのときは完全にステーブルコインであり、pcdのときは完全に担保であるか、pcd ≤ p ≤ pcuのときはAMM価格は現在の価格pに等しくなります。
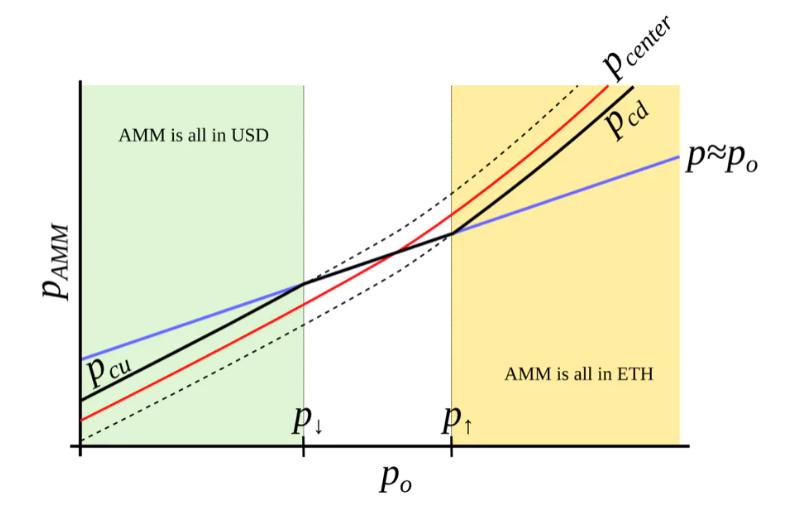図4：私たちが探しているAMM。私たちは、pcdとpcuがpoの関数であり、poが成長するにつれてそれらもさらに成長するようなAMMを構築しようとしています。この場合、このAMMはETHが高価なときはすべてETHであり、ETHが安価なときはすべてUSDになります。
私たちは、Uniswap3と同様に、ボンディングカーブの双曲線の形状を保持するいくつかのバンドから始めます。たとえば、USDの量をx、ETHの量をyとすると、「強化された」定数-製品不変量は次のようになります：
私たちは、Uniswap3と同様に、ボンディングカーブの双曲線の形状を保持するいくつかのバンドから始めます。たとえば、USDの量をx、ETHの量をyとすると、「強化された」定数-製品不変量は次のようになります：
また、x0 ≡ x + fおよびy0 ≡ y + gと表記することもでき、これにより不変量はお馴染みのI = x0 y0として書くことができます。しかし、fとgは一定ではありません：それらは外部価格オラクルの変化に伴って変化します（不変量Iも同様で、オラクル価格poが変わらない限り不変量です）。特定のpoにおいて、fとgはバンド全体で一定です。前述のように、p↑をバンドの上限価格、p↓をバンドの下限価格として表記します。流動性の集中度を測る指標Aを次のように定義します：
また、x0 ≡ x + fおよびy0 ≡ y + gと表記することもでき、これにより不変量はお馴染みのI = x0 y0として書くことができます。しかし、fとgは一定ではありません：それらは外部価格オラクルの変化に伴って変化します（不変量Iも同様で、オラクル価格poが変わらない限り不変量です）。特定のpoにおいて、fとgはバンド全体で一定です。前述のように、p↑をバンドの上限価格、p↓をバンドの下限価格として表記します。流動性の集中度を測る指標Aを次のように定義します：
私たちが探している特性は、より高い価格poが同じバランスでさらに高い価格をもたらすべきであり、現在の市場価格（平均的にはpoに従う）はそれよりも低く、バンドはすべてETHに向かって取引されることです（逆方向も同様です）。これを満たす方法は多くありますが、私たちは次のものが必要です：
私たちが探している特性は、より高い価格poが同じバランスでさらに高い価格をもたらすべきであり、現在の市場価格（平均的にはpoに従う）はそれよりも低く、バンドはすべてETHに向かって取引されることです（逆方向も同様です）。これを満たす方法は多くありますが、私たちは次のものが必要です：
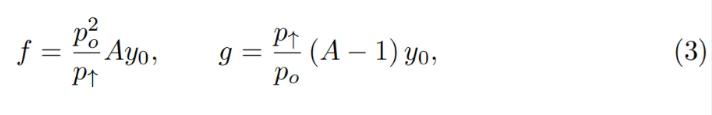
ここでy0は、現在のバンドにおけるETH建ての預金のp0依存の指標であり、現在の価格p、p↑、およびpoが互いに等しいとき、y = y0およびx = 0となるように定義されます（図4のpo = p↑の点を参照）。その時点でyを置き換えると：
ここでy0は、現在のバンドにおけるETH建ての預金のp0依存の指標であり、現在の価格p、p↑、およびpoが互いに等しいとき、y = y0およびx = 0となるように定義されます（図4のpo = p↑の点を参照）。その時点でyを置き換えると：
価格はdx0 /dy0に等しく、したがって定数-製品不変量に対しては：
価格はdx0 /dy0に等しく、したがって定数-製品不変量に対しては：
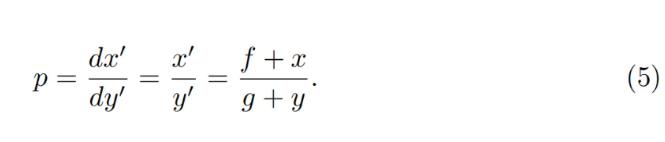
po = p↑またはpo = p↓の状況をx = 0またはy = 0で置き換えることで、上記の式が自己一貫していることを確認できます。
po = p↑またはpo = p↓の状況をx = 0またはy = 0で置き換えることで、上記の式が自己一貫していることを確認できます。
通常、バンドに対してはp↑を知っており、したがってp↓、po、定数A、そしてxとy（バンド内の現在の預金）も知っています。すべてを計算するために、yoを見つける必要があります。これは不変量の二次方程式を解くことで見つけることができます：
通常、バンドに対してはp↑を知っており、したがってp↓、po、定数A、そしてxとy（バンド内の現在の預金）も知っています。すべてを計算するために、yoを見つける必要があります。これは不変量の二次方程式を解くことで見つけることができます：
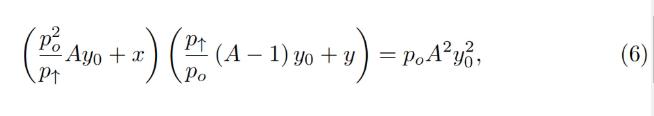
これはyoに対する二次方程式に変わります：
これはyoに対する二次方程式に変わります：
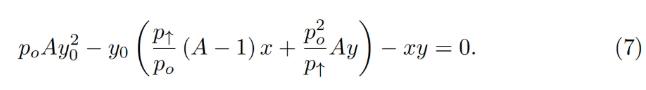
スマートコントラクト内で、get_y0関数でこの二次方程式を解きます。
スマートコントラクト内で、get_y0関数でこの二次方程式を解きます。
オラクル価格poが一定の間、AMMは通常の方法で機能します。つまり、価格が上昇するとETHを売却し、価格が下がるとETHを購入します。「現在の下落」価格pcdに対してx = 0を単純に置き換えたり、「現在の上昇」価格pcuに対してy = 0を置き換えたりすることで、AMM価格がpoの現在の値とp↑の現在の値であることを示すことができます：
オラクル価格poが一定の間、AMMは通常の方法で機能します。つまり、価格が上昇するとETHを売却し、価格が下がるとETHを購入します。「現在の下落」価格pcdに対してx = 0を単純に置き換えたり、「現在の上昇」価格pcuに対してy = 0を置き換えたりすることで、AMM価格がpoの現在の値とp↑の現在の値であることを示すことができます：
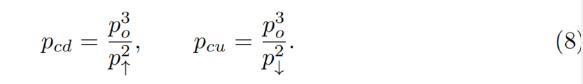
もう一つの実用的に重要な質問は、価格が上昇または下降する場合、オラクル価格poが完全にそれに絶熱的に追従できるほど遅い場合、現在の値xとyを考慮して、バンドは最終的にどれだけのETH（価格が上昇した場合）またはUSD（価格が下落した場合）を持つことになるかです。これは直ちに簡単な数学的問題ではありませんが、数値計算はかなりシンプルな答えを示しました：
もう一つの実用的に重要な質問は、価格が上昇または下降する場合、オラクル価格poが完全にそれに絶熱的に追従できるほど遅い場合、現在の値xとyを考慮して、バンドは最終的にどれだけのETH（価格が上昇した場合）またはUSD（価格が下落した場合）を持つことになるかです。これは直ちに簡単な数学的問題ではありませんが、数値計算はかなりシンプルな答えを示しました：
これらの結果は、ローンの安全性やAMMの潜在的な損失を評価する際に使用します。
これらの結果は、ローンの安全性やAMMの潜在的な損失を評価する際に使用します。
今、私たちは1つのバンドの説明を持っています。すべての価格空間を、価格p↓とp↑で接触するバンドに分割します。したがって、基準価格pbaseを設定し、バンド番号nを持つと：
今、私たちは1つのバンドの説明を持っています。すべての価格空間を、価格p↓とp↑で接触するバンドに分割します。したがって、基準価格pbaseを設定し、バンド番号nを持つと：
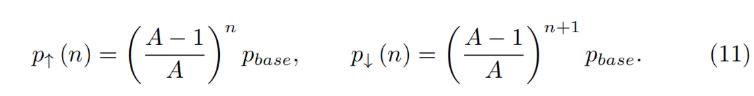
任意のバンドに対する式7と式5の解は次のようになります：
任意のバンドに対する式7と式5の解は次のようになります：
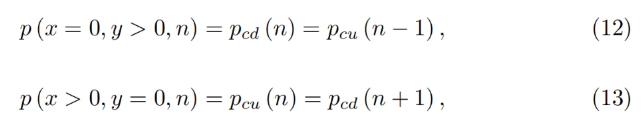
これにより、バンド間に隙間がないことが示されます。
これにより、バンド間に隙間がないことが示されます。
取引は式1の不変性を保持しながら行われますが、AMM内部の現在の価格は価格poが変化するとシフトします：poが下がると上がり、その逆も立方的に行われます（式8から確認できます）。
取引は式1の不変性を保持しながら行われますが、AMM内部の現在の価格は価格poが変化するとシフトします：poが下がると上がり、その逆も立方的に行われます（式8から確認できます）。
LLAMMAとステーブルコイン
ステーブルコインは、ボラティリティのある担保（例えば、ETHに対する暗号通貨）に対してステーブルコインを借りるCDPです。担保は、担保の価格が比較的ゆっくりと下がる場合にCDPを閉じるために必要な十分なステーブルコインに変換されるように、LLAMMAにその価格範囲（そのようなバンド）でロードされます（これは自己清算を介して発生するか、カバレッジが危険な限界に非常に近い場合には外部清算を介して発生する可能性があります）。
ステーブルコインは、ボラティリティのある担保（例えば、ETHに対する暗号通貨）に対してステーブルコインを借りるCDPです。担保は、担保の価格が比較的ゆっくりと下がる場合にCDPを閉じるために必要な十分なステーブルコインに変換されるように、LLAMMAにその価格範囲（そのようなバンド）でロードされます（これは自己清算を介して発生するか、カバレッジが危険な限界に非常に近い場合には外部清算を介して発生する可能性があります）。
ユーザーが担保を預けてステーブルコインを借りると、LLAMMAスマートコントラクトは担保を配置するバンドを計算します。担保の価格が変わると、それはステーブルコインに変換され始めます。システムが「水中」にあるとき、ユーザーはすでにローンをカバーするのに十分なUSDを持っています。取得できるステーブルコインの量は、公開のgetxdownメソッドを使用して計算できます。もしそれが清算閾値に非常に近い値を返す場合、外部清算者が関与する可能性があります（通常、担保価格が下落して横ばいになった後の数日または数週間内には発生しないはずですし、担保価格が決して上昇しないか、比較的早く戻らない場合には決して発生しません）。健康メソッドは、getxdownと債務の比率、および価格が「清算」を大きく上回っているときの担保の価値の増加を返します。
ユーザーが担保を預けてステーブルコインを借りると、LLAMMAスマートコントラクトは担保を配置するバンドを計算します。担保の価格が変わると、それはステーブルコインに変換され始めます。システムが「水中」にあるとき、ユーザーはすでにローンをカバーするのに十分なUSDを持っています。取得できるステーブルコインの量は、公開のgetxdownメソッドを使用して計算できます。もしそれが清算閾値に非常に近い値を返す場合、外部清算者が関与する可能性があります（通常、担保価格が下落して横ばいになった後の数日または数週間内には発生しないはずですし、担保価格が決して上昇しないか、比較的早く戻らない場合には決して発生しません）。健康メソッドは、getxdownと債務の比率、および価格が「清算」を大きく上回っているときの担保の価値の増加を返します。
ステーブルコインが利息を請求する場合、これもAMMに反映されるべきです。これは、すべての価格グリッドを調整することによって行われます。したがって、ステーブルコインが利率rを請求すると、AMM内のすべての価格グリッドは、基準価格の乗数を介して同じ利率rで上方にシフトします。したがって、請求された利率が正である限り、乗数は時間とともに上昇します。
ステーブルコインが利息を請求する場合、これもAMMに反映されるべきです。これは、すべての価格グリッドを調整することによって行われます。したがって、ステーブルコインが利率rを請求すると、AMM内のすべての価格グリッドは、基準価格の乗数を介して同じ利率rで上方にシフトします。したがって、請求された利率が正である限り、乗数は時間とともに上昇します。
getxdownまたはgetyupを計算する際、最初に現在の価格が現在の価格poに移動した場合のステーブルコインと担保の量x∗とy∗を探します。次に、poがそれぞれ最低バンドの最低価格または最高バンドの最高価格に絶熱的に変化した場合に、どれだけのステーブルコインまたは担保を得られるかを見ます。このようにして、現在の瞬時の価格に依存しないステーブルコインの量を測定できます。これは、サンドイッチ攻撃に対する抵抗にとって重要です。
getxdownまたはgetyupを計算する際、最初に現在の価格が現在の価格poに移動した場合のステーブルコインと担保の量x∗とy∗を探します。次に、poがそれぞれ最低バンドの最低価格または最高バンドの最高価格に絶熱的に変化した場合に、どれだけのステーブルコインまたは担保を得られるかを見ます。このようにして、現在の瞬時の価格に依存しないステーブルコインの量を測定できます。これは、サンドイッチ攻撃に対する抵抗にとって重要です。**
**
LLAMMAは、ETH/USD価格として定義されたpoを価格ソースとして使用し、私たちのステーブルコインはペッグの下（ps < 1）またはペッグの上（ps > 1）で取引される可能性があります。もしps < 1であれば、LLAMMA内の価格はp > poです。
LLAMMAは、ETH/USD価格として定義されたpoを価格ソースとして使用し、私たちのステーブルコインはペッグの下（ps < 1）またはペッグの上（ps > 1）で取引される可能性があります。もしps < 1であれば、LLAMMA内の価格はp > poです。
絶熱近似では、p = po/psであり、すべての担保<->ステーブルコインの変換は、より高いオラクル価格で発生します/オラクル価格が低く、次のように等しい場合：
絶熱近似では、p = po/psであり、すべての担保<->ステーブルコインの変換は、より高いオラクル価格で発生します/オラクル価格が低く、次のように等しい場合：
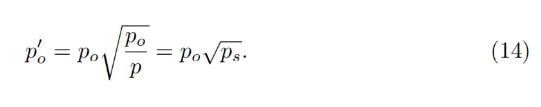
この価格では、変換時に得られるステーブルコインの量は1/psの係数だけ高くなります（もしps < 1であれば）。
この価格では、変換時に得られるステーブルコインの量は1/psの係数だけ高くなります（もしps < 1であれば）。
ps > 1が長時間続くことは望ましくなく、そのために安定器を使用します（次の章を参照）。
ps > 1が長時間続くことは望ましくなく、そのために安定器を使用します（次の章を参照）。
自動安定器と金融政策
自動安定器と金融政策
ps > 1（例えば、ステーブルコインの需要が増加したため）になると、安定保持のための準備金が形成され、ステーブルコインと可赎回の基準コインまたはLPトークンとの間の非対称な預金によってCurveプールに入ります。ps > 1になると、PegKeeperコントラクトは無担保のステーブルコインを鋳造し（のみ！）、最終的な価格が1を下回らないように、単側でstableswapプールに預け入れることが許可されます。ps < 1の場合、PegKeeperは（非対称に）引き出し、ステーブルコインを焼却することが許可されます。
ps > 1（例えば、ステーブルコインの需要が増加したため）になると、安定保持のための準備金が形成され、ステーブルコインと可赎回の基準コインまたはLPトークンとの間の非対称な預金によってCurveプールに入ります。ps > 1になると、PegKeeperコントラクトは無担保のステーブルコインを鋳造し（のみ！）、最終的な価格が1を下回らないように、単側でstableswapプールに預け入れることが許可されます。ps < 1の場合、PegKeeperは（非対称に）引き出し、ステーブルコインを焼却することが許可されます。
これらの行動は、価格psが1を超えると急速に減価し、1を下回ると価値が上がる原因となります。非対称な預金と引き出しが価格を変えるからです。鋳造が無担保であっても、ステーブルコインはステーブルコインプールの流動性によって暗黙的に担保されているように見えます。鋳造/焼却のサイクル全体は、最終的には安定性を提供しながら利益をもたらすように見えます。
これらの行動は、価格psが1を超えると急速に減価し、1を下回ると価値が上がる原因となります。非対称な預金と引き出しが価格を変えるからです。鋳造が無担保であっても、ステーブルコインはステーブルコインプールの流動性によって暗黙的に担保されているように見えます。鋳造/焼却のサイクル全体は、最終的には安定性を提供しながら利益をもたらすように見えます。
安定器に鋳造されたステーブルコインの量（債務）をdstとし、stableswap AMMでステーブルコインを購入するために必要な可赎回USDの量を計算する関数をfdx()とします。したがって、準備金をあまり大きくしないために、借入rを変動させる「遅い」安定化メカニズムを使用します：
安定器に鋳造されたステーブルコインの量（債務）をdstとし、stableswap AMMでステーブルコインを購入するために必要な可赎回USDの量を計算する関数をfdx()とします。したがって、準備金をあまり大きくしないために、借入rを変動させる「遅い」安定化メカニズムを使用します：
ここでhは、rが2倍の要因で変化するpsの変化です（高いpsは低いrをもたらします）。安定器の債務dstの量は、ps = 1のr0に応じて異なる値で均衡します。したがって、手動で設定する代わりに、dst/supplyがある目標数（例えば5%）より大きい間はr0を減少させることができます（これにより、借り手がステーブルコインを借りて投げ捨てることを奨励し、その価格を下げ、システムにdstを焼却させる）または、低い場合は増加させることができます（これにより、借り手がローンを返済し、psを押し上げ、システムに債務dstと安定器の預金を増加させることを強制します）。
ここでhは、rが2倍の要因で変化するpsの変化です（高いpsは低いrをもたらします）。安定器の債務dstの量は、ps = 1のr0に応じて異なる値で均衡します。したがって、手動で設定する代わりに、dst/supplyがある目標数（例えば5%）より大きい間はr0を減少させることができます（これにより、借り手がステーブルコインを借りて投げ捨てることを奨励し、その価格を下げ、システムにdstを焼却させる）または、低い場合は増加させることができます（これにより、借り手がローンを返済し、psを押し上げ、システムに債務dstと安定器の預金を増加させることを強制します）。
結論
提示されたメカニズムは、ステーブルコインの製造および借入目的の清算リスクを解決できることを期待しています。さらに、安定器および自動金融政策メカニズムは、過度に大きなPSMを保持することなく、ペッグを維持するのに役立つことができます。
提示されたメカニズムは、ステーブルコインの製造および借入目的の清算リスクを解決できることを期待しています。さらに、安定器および自動金融政策メカニズムは、過度に大きなPSMを保持することなく、ペッグを維持するのに役立つことができます。
