Detailed Explanation of the Two Verification States of Rollup: Fraud Proof and Non-Interactive Fraud Proof

Original Title: 《Truly Understanding Layer2》

Original Author: web3 Explorer

The core goal of Layer2 is to enhance the processing speed of blockchain, as it is impossible to satisfy security, processing speed, and decentralization (the impossible triangle) simultaneously in Layer 1.

There are three modes of L2: state channels, plasma, and rollup. Due to their respective shortcomings, none of them have become the main focus, so this article will only introduce the rollup mechanism. Other modes can be researched independently if interested.

1. Rollup

The core idea of Rollup is to keep a proof that can verify the transaction process on L1, while storing and running the transaction process (computational process) and state on L2.

What is the proof of the transaction process? We know that the process of executing a transaction is the process of transitioning from one state to another. If L1 knows a set of states before the transaction and a set of states after the transaction, along with this set of transactions, it can naturally verify whether the state transition corresponding to this set of transactions is correct.

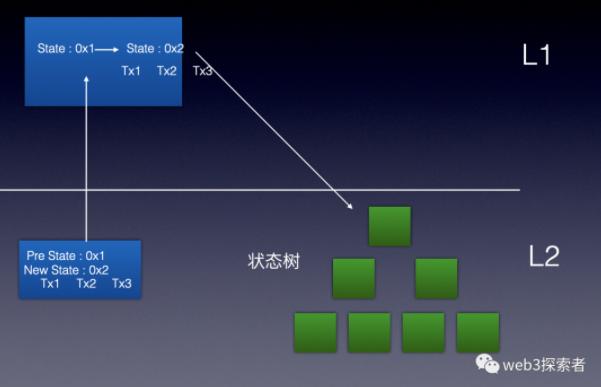
As shown in the figure above, the publisher submits the root hash of the state tree before the transaction, the root hash of the state tree after the transaction, and the transaction to L1. The L1 smart contract confirms whether the root hash of the state tree before the transaction matches the stored root hash. If the root hash before the transaction matches, it indicates that the initial state is correct. So how do we verify whether the transaction process is correct? The safest approach would be to re-execute the L2 transaction tree on L1 each time to perform the state transition, but this would defeat the purpose of L2 and still face the issue of processing speed in the impossible triangle.

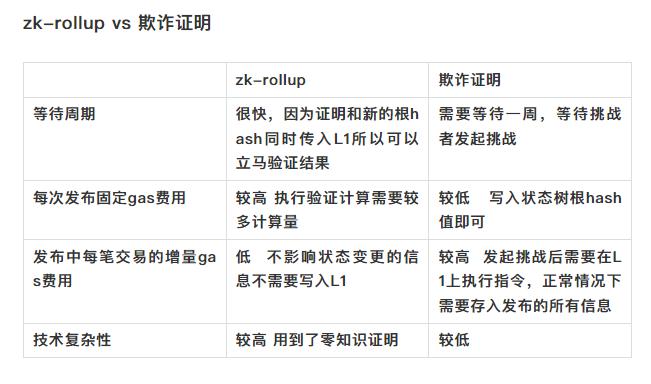
How to verify whether the state transition is correct leads to two different Layer2 Rollup mechanisms.

The first is fraud proof, which assumes that the stored state is correct by default and waits for other participants to challenge with fraud proofs. Each time L2 publishes to L1, the nodes must pay a certain deposit. When fraud is proven, it rolls back to the previous state, and the publisher's deposit will be completely deducted, with part given to the challenger and part directly destroyed. How to prove fraud is divided into interactive fraud proof and non-interactive fraud proof, depending on the degree of interaction with L1, which will be explained in detail below.

The second is zero-knowledge proof, where each time a state is submitted, a proof must be provided, and the proof will be verified on L1. If the verification of the root hash is correct, it indicates that the publisher's submission is accurate. The proof here utilizes research related to zero-knowledge proofs.

• Fraud Proof

As mentioned above, fraud proof operates on the principle of default trust. When there are no challenges, the process is relatively simple, which is to store the root hash of the state tree and transaction information in L1. The core issue arises when a challenger initiates a challenge, how to prove that the root hash of the state tree before the transaction can be transformed into the new state root hash through this set of transactions. There are two approaches here.

1. Non-interactive fraud proof, which involves re-executing this set of transactions on L1 to see if the resulting state tree's root hash matches the input root.

2. Interactive fraud proof, where the challenger and the publisher engage in multiple rounds of challenges on L2, ultimately allowing the challenger to identify which specific instruction is fraudulent, with L1 making the final judgment. L1 only needs to execute the minimum instruction that is disputed.

• Non-interactive Fraud Proof

We will use Optimism as an example to illustrate interactive fraud.

Analysis of the Fraud Proof Process:

Non-interactive fraud proof is relatively simple to implement. It involves executing the transactions performed in L2 again in L1 to determine whether the root hash of the state matches to identify fraudulent behavior.

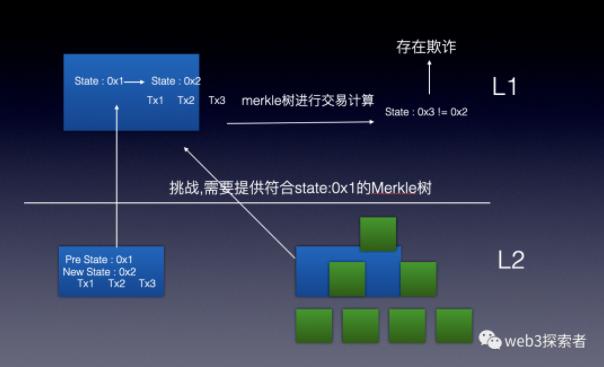
As shown in the figure above, the publisher publishes information to L1, carrying transaction information and the overall new and old root hashes. When the smart contract in L1 receives this, it will default to changing the state to the new root hash. At this point, the challenger raises a challenge, and the challenger needs to provide a Merkle state tree that corresponds to the old root hash. The L1 smart contract executes the complete transaction process using the old state tree to obtain the root hash and compares it with the new root hash provided by the publisher. If they are not equal, it indicates fraudulent behavior.

Re-execution will encounter a problem, as block-related attributes may change due to different execution environments.

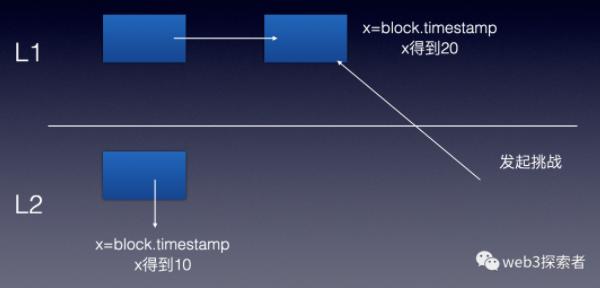
As shown in the figure above, block.timestamp will obtain the current block's timestamp, but due to the different environments in which contracts are executed, the obtained timestamps are likely to be different. Let's see how Optimism designs OVM to solve this problem.

OVM

To address the inconsistency of the environment when running smart contracts on L2 and L1, Optimism uses virtualization technology (essentially using encapsulation methods to shield) to allow smart contracts to directly obtain some states that are called after being encapsulated by OVM.

In the previous example, block.timestamp cannot be called directly; instead, it is replaced with a method encapsulated by OVM, ovm_getTimestamp (a non-real arbitrary name).

Interactive Fraud Proof

We will use Arbitrum as an example to illustrate interactive fraud.

Analysis of the Arbitrum Fraud Proof Process:

In fact, the earlier article on smart contracts mentioned that the execution process of smart contracts is essentially a process of advancing state changes. Let's revisit the concept of a state machine:

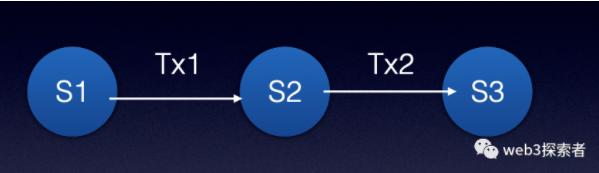
As shown in the figure, whether on the state tree of L1 or L2, it is driven by a series of transactions (the execution of a smart contract is also a call of a transaction) that push the state transition. Due to smart contracts, transactions can also be broken down into smaller instruction steps. Thus, it becomes the following form:

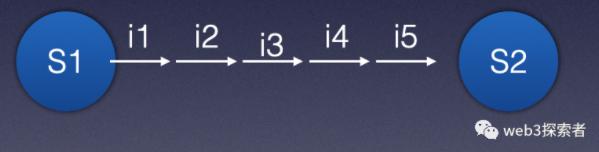
Our problem transforms into proving that the state tree transitions from state A to state B through N instructions. Is this proof process decomposable? Using a divide-and-conquer approach, we can think of a binary method, breaking one large problem into two sub-problems. The problem becomes proving that state A transitions to state X through the first N/2 instructions and that state X transitions to state B through the last N/2 instructions. Gradually halving will ultimately pinpoint the problematic instruction, which can then be verified by L1.

Let's describe the entire execution process. Assume X is the publisher who publishes the transition from state A to state B through N instructions, and Y is the challenger.

Y challenges X, requesting the state at the N/2 instruction point. After X provides the state, Y will verify its correctness. If the verification is correct, it indicates that the first N/2 instructions executed without issues, and the problem lies in the last N/2. If the verification is incorrect, it indicates that there is an issue with the execution of the first N/2 instructions. Y continues to ask X for the state at the problematic instruction interval N/2, repeating this process until the problematic instruction is found (this does not mean the instruction itself is problematic, but rather that the state before executing the instruction cannot be transformed into the state after executing the instruction).

In practical applications, Arbitrum does not use a binary method but employs a K-way division, dividing N instructions into N/K groups to find fraudulent instructions, which is more efficient.

AVM

The core difference in the design of AVM compared to EVM is that AVM not only needs to support EVM-compatible execution logic but also needs to support the proof logic of interactive fraud proof.

During the proof process, it is essential to ensure the correctness of the instructions in the current program counter. A blockchain-like approach is taken here, where the PC (current program counter position) stores not only the opcode but also the hash value at PC+1, allowing for verification of each instruction's correctness during execution.

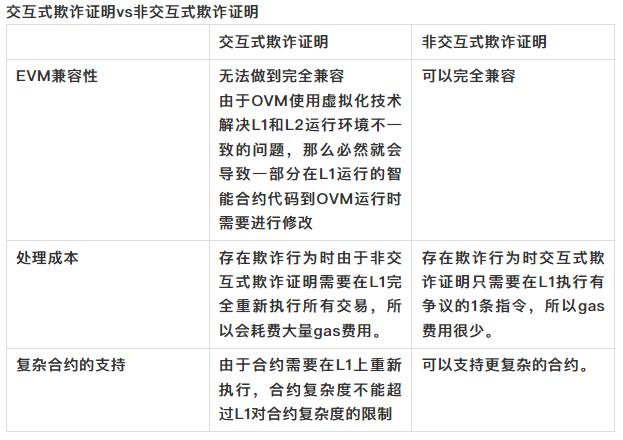
From the above comparison, it can be seen that interactive fraud proof, despite its higher implementation difficulty, has superior main features compared to non-interactive fraud proof. The representative user of non-interactive fraud proof, Optimism, is also preparing to switch to interactive fraud proof. It can be anticipated that interactive fraud proof will become the mainstream of fraud proof in the future.

Fraud proofs generally have a problem of long withdrawal periods, as they require sufficient time for challengers to raise challenges. Benefiting from recent advancements in cryptography, zk-rollup will address this issue.

2. ZK-Rollup

• Meaning of Zero-Knowledge Proof

Zero-knowledge means that participants can solve a problem without revealing the result to the verifier, allowing the verifier to believe that the participant's solution is correct. Here are two well-known examples.

• The Famous Alibaba

A long time ago, there was a cave hidden with treasures, and Alibaba was captured by robbers because he knew the incantation to open the stone door of the cave. If he reveals the incantation, it loses its value, and he will die; if he refuses to speak, the robbers will also kill him.
In this dilemma, Alibaba came up with a clever plan. He instructed the robbers randomly: "You only need to stand an arrow's distance away from me, pointing your bows at me. If you raise your right hand, I will recite the incantation to open the stone door; if you raise your left hand, I will recite the incantation to close the stone door. If I fail to do so or attempt to escape, you can shoot me with your arrows."
After repeating this several times, the robbers could never learn the incantation but could believe that Alibaba indeed possessed it, and Alibaba saved his life.

• The Sudoku Problem

There is a 9x9 Sudoku puzzle, and A has solved the answer. A wants B to believe that A has successfully solved it without revealing the answer.

The solution is: B randomly selects a row or column, and A takes this row or column, shuffles it, and presents it to B, containing numbers 1 to 9. After repeating this multiple times, B will believe that A has arrived at the correct answer.

• How ZK-SNARK Solves the Problem

Currently, the more mature ZK mechanism is zk-SNARK, so the zk algorithm mentioned later will take zk-SNARK as an example.

The workflow of ZK-SNARK consists of two steps:

1. Transforming the problem into a circuit and then into a polynomial, i.e., converting the real zero-knowledge proof problem into a mathematical zero-knowledge proof problem.

2. Verifying this polynomial zero-knowledge proof by randomly providing some checkpoints to derive a solution that meets the conditions, thus validating the proof.

We will introduce zk proof in a separate article later, as zk proof will not only be applied in Ethereum scaling but also in privacy protection fields, such as the increasingly popular DID.

Using Starkware as an example, we will introduce the mechanism of zk-rollup, as shown in the flowchart below.

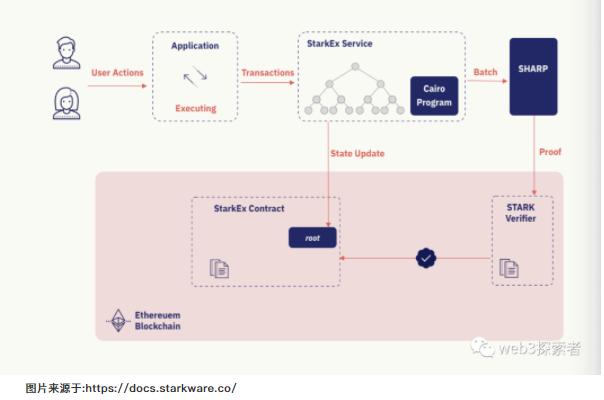
When the publisher submits a transaction to L1, they need to package the transaction and the state on L2 and hand it over to a proof generation service. The proof generation service performs extensive calculations to generate the proof for this submission. The proof service sends the proof to the verification service on L1. Meanwhile, the publisher submits the state root hash to L1. Upon receiving the root hash, L1 will inquire the verification service on L1, which will verify the root hash based on the proof. If correct, L1 will switch the state root to the new hash value.

In this process, verifying the root hash of the state tree originally required executing all transactions of this submission from the previous complete state tree to obtain a new transaction tree, thereby calculating the new root hash. Ultimately, the validity of the submission is determined by comparing the root hash provided by the publisher with the new hash value. With the introduction of zk proof, we do not need to know the specific states and transactions to determine whether the hash value is correct. This is the application of zk proof in Ethereum scaling.

• Development of ZK Proof

Comparison between SNARK (Zero-Knowledge Succinct Non-Interactive Argument of Knowledge) and STARK (Zero-Knowledge Scalable Transparent Argument of Knowledge):

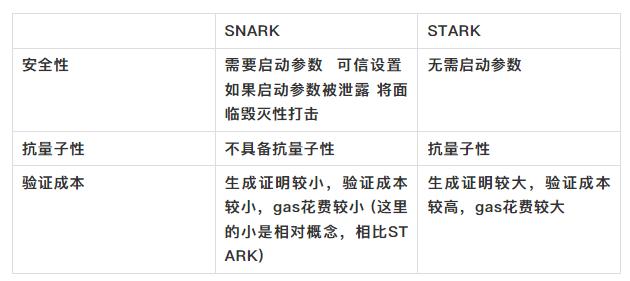
Compared to SNARK, STARK is still in its early stages of development, but it shows better performance in security and quantum resistance, and is expected to achieve greater development in the future.

3. Conclusion

In this article, we primarily introduced the mainstream Layer2 technology of rollups. Rollups are divided into fraud proof and zk rollups based on when to verify the correctness of the L2 submitted state. Fraud proof is further divided into non-interactive fraud proof and interactive fraud proof based on whether challengers need to interact with the publisher. The comparison shows that interactive fraud proof has advantages in terms of operational costs and EVM compatibility. The newer cryptographic research results of zk provide us with a new direction, allowing zk rollups to verify the publisher's submissions more quickly. Moreover, zk also brings new possibilities for privacy protection and other areas.